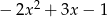/Szkoła średnia/Funkcje

Zadanie nr 4947606

Dodaj do ulubionych
Dodaj do rozwiązanych

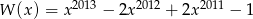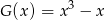Wyznacz resztę z dzielenia wielomianu 2013 2012 2011 W (x) = x − 2x + 2x − 1 przez wielomian G (x) = x3 − x .

Rozwiązanie

Reszta z dzielenia przez wielomian stopnia 3 jest wielomianem kwadratowym, więc szukamy rozkładu postaci

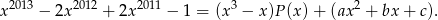
x2013 − 2x2012 + 2x 2011 − 1 = (x 3 − x )P(x) + (ax2 + bx + c).

Podstawiamy teraz w tej równości kolejno 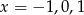x = −1 ,0,1 (czyli miejsca zerowe 3 x − x ). Otrzymujemy w ten sposób układ równań

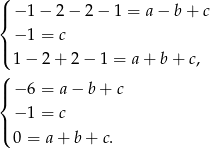
( |{ −1 − 2 − 2 − 1 = a− b + c −1 = c |( ( 1− 2 + 2 − 1 = a+ b+ c, | −6 = a− b+ c { | −1 = c ( 0 = a+ b+ c.

Podstawiając 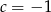c = − 1 w pierwszym i trzecim równaniu mamy

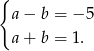
{ a − b = − 5 a + b = 1 .

Dodając te równania stronami mamy 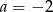a = − 2 , skąd 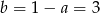b = 1 − a = 3 . Zatem szukana reszta to

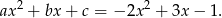
2 2 ax + bx + c = − 2x + 3x − 1 .

 
Odpowiedź: 2 − 2x + 3x − 1

Wersja PDF