Zadanie nr 4968105
Wyznacz wzór funkcji liniowej 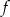 wiedząc, że zbiorem rozwiązań nierówności
wiedząc, że zbiorem rozwiązań nierówności 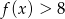 jest przedział
jest przedział 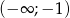 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 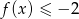 jest przedział
jest przedział 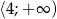 .
.
Rozwiązanie
Sposób I
Szukamy funkcji postaci 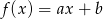 . Rozwiążmy podane w treści nierówności
. Rozwiążmy podane w treści nierówności
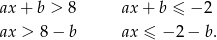
Chcemy teraz podzielić przez  . Ze względu na podane rozwiązania tych nierówności, widać, że musi być
. Ze względu na podane rozwiązania tych nierówności, widać, że musi być 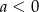 – to jest jedyny sposób, żeby rozwiązaniem pierwszej nierówności był zbiór
– to jest jedyny sposób, żeby rozwiązaniem pierwszej nierówności był zbiór 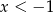 . Zatem dzieląc zmieniamy znak nierówności.
. Zatem dzieląc zmieniamy znak nierówności.
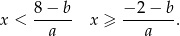
Jeżeli ponownie spojrzymy na podane rozwiązania tych nierówności to dostajemy układ równań.
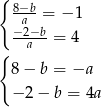
Odejmujemy od pierwszego równania drugie (żeby skrócić 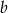 ) i mamy
) i mamy
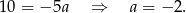
Z pierwszego równania mamy
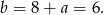
Sposób II
Zadanie możemy też rozwiązać bardziej geometrycznie. Jeżeli narysujemy sobie proste 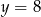 i
i 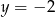 , to patrząc na obrazek widać, że szukana prosta musi mieć
, to patrząc na obrazek widać, że szukana prosta musi mieć 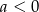 oraz musi przecinać prostą
oraz musi przecinać prostą 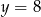 w punkcie
w punkcie 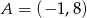 , a prostą
, a prostą 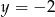 w punkcie
w punkcie 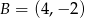 .
.
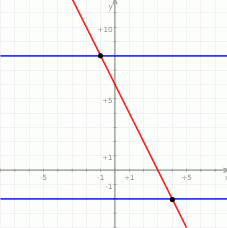
Szukamy zatem prostej przechodzącej przez te dwa punkty. Możemy to zrobić, jak w poprzednim sposobie, układem równań, lub możemy od razu skorzystać ze wzoru na prostą przechodzącą przez dwa punkty 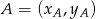 i
i 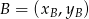 :
:
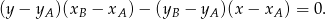
Mamy zatem
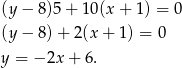
Odpowiedź: