/Szkoła średnia/Funkcje

Zadanie nr 5477834

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 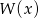W (x) przy dzieleniu przez dwumiany 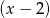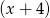(x − 2) , (x+ 4) daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu 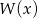W (x) przez wielomian 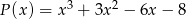P(x ) = x3 + 3x2 − 6x − 8 , wiedząc, że liczba -1 jest miejscem zerowym wielomianu W (x ) .

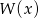Rozwiązanie

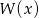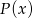Reszta z dzielenia W (x) przez P (x) jest wielomianem stopnia 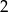2 , mamy zatem

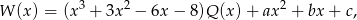
W (x) = (x3 + 3x 2 − 6x − 8)Q (x)+ ax2 + bx+ c,

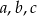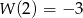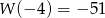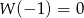dla pewnych a ,b,c . Wiemy ponadto, że W (2) = − 3 , W (− 4) = − 51 oraz W (−1 ) = 0 . Wstawiając te wartości w powyższej równości otrzymujemy układ równań

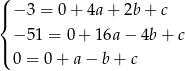
( | − 3 = 0 + 4a + 2b + c { | − 51 = 0+ 1 6a− 4b+ c ( 0 = 0 + a − b + c

Odejmując od drugiego równania pierwsze, a od pierwszego trzecie (żeby poskracać c i maksymalnie zmniejszyć wpółczynnik przy a ), mamy

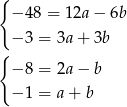
{ − 48 = 12a − 6b − 3 = 3a + 3b { − 8 = 2a − b − 1 = a + b

Dodając do pierwszego równania drugie, mamy 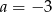a = − 3 . Stąd 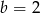b = 2 i c = 5 .  
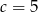Odpowiedź: − 3x2 + 2x + 5

Wersja PDF