Zadanie nr 5506193
Oblicz wartość wyrażenia 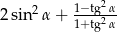 , gdzie
, gdzie  jest kątem ostrym.
jest kątem ostrym.
Rozwiązanie
Skorzystamy z definicji tangensa
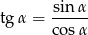
i jedynki trygonometrycznej
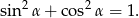
Liczymy
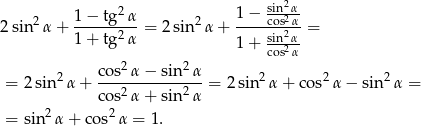
Odpowiedź: 1
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz wartość wyrażenia 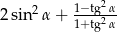 , gdzie
, gdzie  jest kątem ostrym.
jest kątem ostrym.
Skorzystamy z definicji tangensa
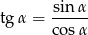
i jedynki trygonometrycznej
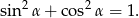
Liczymy
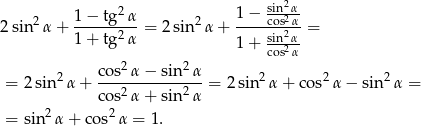
Odpowiedź: 1
