/Szkoła średnia/Funkcje

Zadanie nr 5720686

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 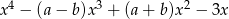4 3 2 x − (a− b)x + (a+ b)x − 3x jest podzielny przez wielomian 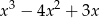x 3 − 4x 2 + 3x . Oblicz a i b .

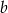Rozwiązanie

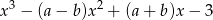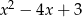Oba wielomiany są podzielne przez x , więc możemy je skrócić przez ten wspólny czynnik i zostaje nam podzielność x3 − (a− b)x2 + (a+ b)x − 3 przez x 2 − 4x + 3 . Rozłóżmy ten drugi trójmian na czynniki.

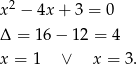
x2 − 4x+ 3 = 0 Δ = 16 − 1 2 = 4 x = 1 ∨ x = 3.

Wiemy zatem, że

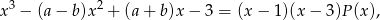
x3 − (a − b)x2 + (a + b)x − 3 = (x − 1 )(x − 3)P(x),

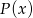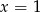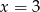dla pewnego wielomianu P (x) . Ponieważ prawa strona zeruje się dla x = 1 i x = 3 , tak samo musi być z lewą stroną, co prowadzi do układu równań.

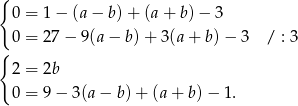
{ 0 = 1− (a− b )+ (a + b) − 3 0 = 27− 9(a− b)+ 3(a+ b)− 3 / : 3 { 2 = 2b 0 = 9− 3(a− b)+ (a + b) − 1.

Z pierwszego równania mamy 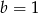b = 1 , co po wstawieniu do drugiego daje nam

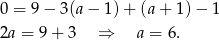
0 = 9 − 3(a − 1) + (a + 1) − 1 2a = 9 + 3 ⇒ a = 6.

 
Odpowiedź: a = 6 ,b = 1

Wersja PDF