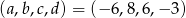/Szkoła średnia/Funkcje

Zadanie nr 6045199

Dodaj do ulubionych
Dodaj do rozwiązanych

Reszta z dzielenia wielomianu 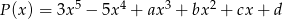5 4 3 2 P(x) = 3x − 5x + ax + bx + cx + d przez wielomian 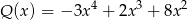Q(x ) = − 3x4 + 2x3 + 8x2 jest taka sama jak reszta z dzielenia wielomianu 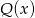Q (x) przez wielomian 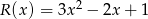R (x) = 3x 2 − 2x + 1 . Oblicz wartości współczynników 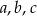a,b,c i d .

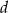Rozwiązanie

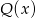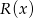Obliczmy najpierw resztę z dzielenia wielomianu Q (x) przez R (x) . Można to zrobić na różne sposoby, my zrobimy to grupując wyrazy.

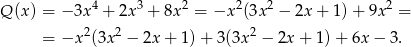
Q (x) = − 3x4 + 2x 3 + 8x 2 = −x 2(3x2 − 2x + 1) + 9x 2 = 2 2 2 = −x (3x − 2x + 1)+ 3 (3x − 2x + 1) + 6x − 3.

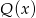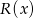W takim razie reszta z dzielenia Q(x ) przez R(x ) jest równa 6x − 3 .

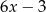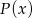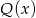Dzielimy teraz wielomian P (x) przez Q (x) – ponownie zrobimy to grupując wyrazy.

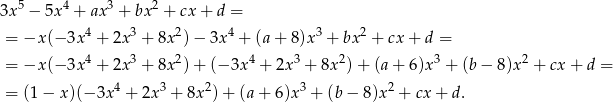
3x5 − 5x4 + ax3 + bx 2 + cx + d = 4 3 2 4 3 2 = −x (− 3x + 2x + 8x )− 3x + (a+ 8)x + bx + cx+ d = = −x (− 3x4 + 2x 3 + 8x 2)+ (− 3x 4 + 2x3 + 8x2)+ (a+ 6)x3 + (b− 8)x2 + cx + d = = (1 − x)(− 3x4 + 2x 3 + 8x 2)+ (a + 6 )x3 + (b − 8 )x2 + cx+ d.

Z drugiej strony wiemy, że otrzymana reszta ma być równa 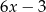6x − 3 , więc mamy układ równań.

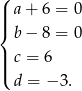
( ||| a + 6 = 0 { b − 8 = 0 |||( c = 6 d = − 3.

Zatem 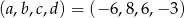(a,b,c,d) = (− 6,8,6 ,− 3 )  
Odpowiedź: (a,b,c,d) = (−6 ,8,6,− 3)

Wersja PDF