/Szkoła średnia/Funkcje

Zadanie nr 6262370

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 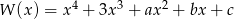4 3 2 W (x) = x + 3x + ax + bx + c jest podzielny przez trójmian 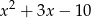x 2 + 3x − 1 0 , a przy dzieleniu przez dwumian 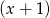(x+ 1) daje resztę -36. Wyznacz współczynniki 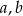a,b i c wielomianu.

Rozwiązanie

Rozłóżmy najpierw podany trójmian na czynniki.

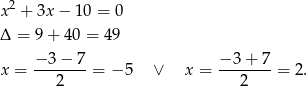
2 x + 3x − 10 = 0 Δ = 9+ 40 = 49 − 3− 7 − 3+ 7 x = -------= − 5 ∨ x = ------- = 2. 2 2

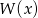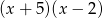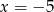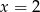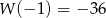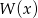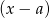Zatem wiemy, że wielomian W (x) jest podzielny przez (x + 5)(x − 2) , czyli liczby x = − 5 i x = 2 są jego pierwiastkami. Wiemy ponadto, że W (−1 ) = − 36 (bo reszta z dzielenia W (x) przez (x− a) jest równa 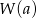W (a) ). Otrzymujemy zatem układ równań

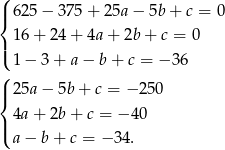
( |{ 6 25− 375 + 25a − 5b + c = 0 | 1 6+ 24+ 4a+ 2b+ c = 0 ( 1 − 3 + a − b + c = − 36 ( |{ 2 5a− 5b+ c = − 250 4a + 2b + c = − 40 |( a − b + c = − 34 .

Odejmujemy od pierwszego i od drugiego równania trzecie (żeby pozbyć się w tych równaniach c ).

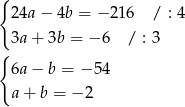
{ 24a − 4b = − 216 / : 4 3a + 3b = − 6 / : 3 { 6a − b = − 54 a + b = − 2

Teraz dodajemy równania stronami (żeby zredukować 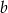b ).

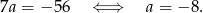
7a = − 5 6 ⇐ ⇒ a = − 8.

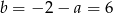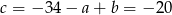Zatem b = − 2 − a = 6 i c = − 34− a+ b = − 20 .  
Odpowiedź: (a,b,c) = (− 8 ,6 ,−2 0)

Wersja PDF