/Szkoła średnia/Funkcje

Zadanie nr 6841842

Dodaj do ulubionych
Dodaj do rozwiązanych

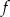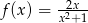Funkcja f określona jest wzorem -2x- f(x ) = x2+1 .

  • Wykaż, że funkcja 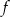f jest nieparzysta.
  • Wykaż, że zbiór wartości funkcji 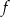f zawiera się w zbiorze ⟨− 1;1⟩ .

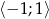Rozwiązanie

  • Liczymy
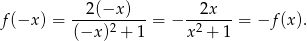
    --2(−x--)-- --2x--- f(−x ) = (−x )2 + 1 = − x2 + 1 = −f (x).
  •  

    Sposób I

    Musimy uzasadnić nierówności

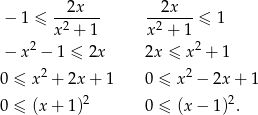
    2x 2x − 1 ≤ ------- -------≤ 1 x2 + 1 x2 + 1 − x2 − 1 ≤ 2x 2x ≤ x2 + 1 2 2 0 ≤ x + 2x + 1 0 ≤ x − 2x + 1 0 ≤ (x + 1)2 0 ≤ (x − 1)2.

    Mnożąc przez mianowniki skorzystaliśmy z tego, że są one dodatnie. Otrzymane nierówności są oczywiście prawdziwe, co dowodzi tezy (bo są równoważne nierównościom, które mieliśmy udowodnić).

    Sposób II

    Liczymy pochodną funkcji f .

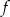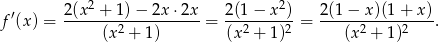
    2 2 f′(x) = 2(x--+-1)-−-2x-⋅2x- = 2(1-−-x--)= 2(1-−-x-)(1-+-x-). (x 2 + 1 ) (x 2 + 1 )2 (x 2 + 1 )2

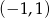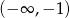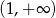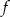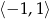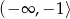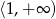    Widać teraz, że pochodna jest dodatnia na zbiorze (− 1,1) i ujemna na przedziałach: (− ∞ ,− 1) i (1,+ ∞ ) . To oznacza, że funkcja f rośnie na przedziale ⟨− 1,1⟩ oraz maleje na każdym z przedziałów: (− ∞ ,− 1⟩ i ⟨1,+ ∞ ) . Mamy ponadto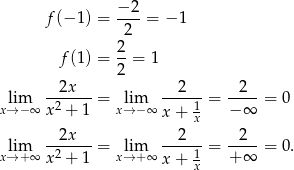

    −2 f(− 1) = ---= − 1 2 f(1) = 2-= 1 2 --2x--- --2--- -2-- x→lim− ∞ x2 + 1 = xl→im−∞ x+ 1 = − ∞ = 0 x lim --2x---= lim --2---= -2--= 0. x→ + ∞ x2 + 1 x→ +∞ x+ 1 + ∞ x

    Te informacje pozwalają naszkicować wykres funkcji.

    PIC

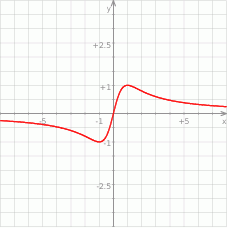
    Teraz powinno być jasne, że rzeczywiście

    x ≤ −1 ⇒ f(x) ∈ ⟨f(− 1 ),f (− ∞ )) = ⟨− 1,0) x ∈ ⟨− 1,1⟩ ⇒ f(x) ∈ ⟨f(− 1),f (1)⟩ = ⟨− 1,1⟩ x ≥ 1 ⇒ f(x) ∈ (f (+∞ ),f (1)⟩ = (0,1⟩.
Wersja PDF