/Szkoła średnia/Funkcje

Zadanie nr 7097014

Dodaj do ulubionych
Dodaj do rozwiązanych

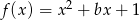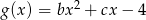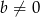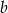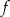Dane są dwie funkcje kwadratowe 2 f(x) = x + bx + 1 oraz 2 g (x) = bx + cx − 4 , gdzie b ⁄= 0 . Wyznacz wszystkie wartości parametrów b i c tak, aby funkcja f miała jedno miejsce zerowe i jednocześnie funkcja 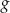g przyjmowała wartości ujemne dla każdego x ∈ R .

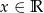Rozwiązanie

Skoro funkcja 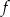f ma mieć dokładnie jedno miejsce zerowe, to musi być

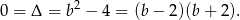
0 = Δ = b2 − 4 = (b− 2)(b+ 2).

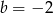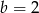Zatem b = − 2 lub b = 2 . Jeżeli jednak 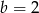b = 2 , to funkcja 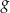g ma dodatni współczynnik przy 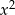x2 i na pewno przyjmuje wartości dodatnie. Zatem 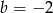b = −2 i mamy

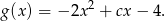
2 g(x) = − 2x + cx − 4 .

Parabola będąca wykresem tej funkcji ma w całości znajdować się poniżej osi 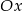Ox , czyli

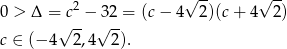
2 √ -- √ -- 0 > Δ = c--− 32-= (c− 4 2 )(c+ 4 2) c ∈ (− 4√ 2,4√ 2 ).

 
Odpowiedź: √ -- √ -- b = − 2 , c ∈ (− 4 2,4 2)

Wersja PDF