/Szkoła średnia/Funkcje

Zadanie nr 7117391

Dodaj do ulubionych
Dodaj do rozwiązanych

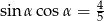Wykaż, że nie istnieje kąt α , dla którego spełniona jest równość sin α cosα = 45 .

Rozwiązanie

Sposób I

Korzystamy ze wzoru na 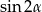sin 2α .

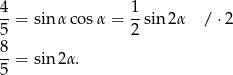
4 1 --= sin α cosα = --sin 2α / ⋅2 5 2 8-= sin 2α. 5

To jednak jest niemożliwe, bo zawsze 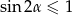sin 2α ≤ 1 .

Sposób II

Podnieśmy daną równość do kwadratu tak, żeby móc skorzystać z jedynki trygonometrycznej.

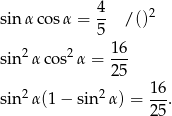
4 sin αco sα = -- / ()2 5 2 2 16- sin αco s α = 25 16 sin2 α(1 − sin2α) = --. 25

Podstawmy 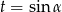t = sin α .

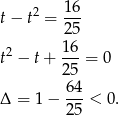
t− t2 = 16- 25 2 16 t − t + 25-= 0 Δ = 1− 64-< 0 . 25

Otrzymana sprzeczność, dowodzi, że warunek 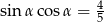4 sin αco sα = 5 nie może być spełniony.

Wersja PDF