Zadanie nr 7205400
Funkcja 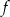 jest określona wzorem
jest określona wzorem 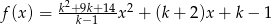 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 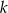 , dla których funkcja
, dla których funkcja 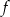 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Rozwiązanie
Ze względu na 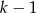 w mianowniku musi być oczywiście
w mianowniku musi być oczywiście 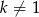 . Rozłóżmy na początek trójmian w liczniku współczynnika przy
. Rozłóżmy na początek trójmian w liczniku współczynnika przy 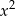 .
.
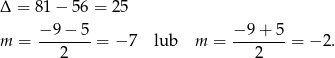
Zatem
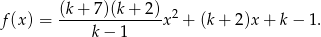
Funkcja ma przyjmować wartość największą, więc współczynnik przy 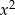 musi być ujemny. Mamy więc
musi być ujemny. Mamy więc
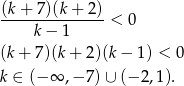
Sprawdźmy teraz, kiedy funkcja ma dwa miejsca zerowe.
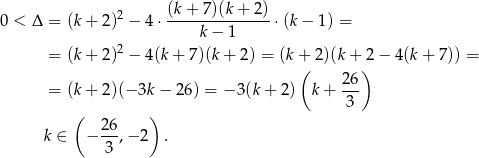
Przy tym założeniu możemy zapisać wzory Viète’a.
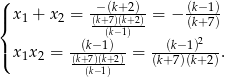
Pierwiastki mają takie same znaki wtedy i tylko wtedy, gdy ich iloczyn jest dodatni (na szczęście nie musimy się zastanawiać jaki jest znak zera, bo dla 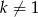 pierwiastki danego równania są niezerowe). Mamy więc nierówność
pierwiastki danego równania są niezerowe). Mamy więc nierówność
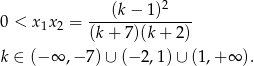
Łącząc wszystkie otrzymane warunki mamy
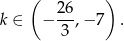
Ponieważ interesują nas tylko wartości całkowite 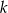 , mamy stąd
, mamy stąd 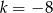 .
.
Odpowiedź: