/Szkoła średnia/Funkcje

Zadanie nr 7263813

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wzór ogólny funkcji kwadratowej, której największą wartością jest 2, a miejscami zerowymi są liczby 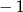− 1 i 3.

Rozwiązanie

Sposób I

Podane miejsca zerowe oznaczają, że funkcja 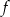f ma wzór postaci

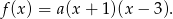
f(x ) = a(x + 1)(x − 3).

Wiemy ponadto, że funkcja ta przyjmuje wartość największą, więc 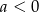a < 0 (ramiona paraboli muszą być skierowane w dół). W takiej sytuacji funkcja 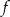f przyjmuje wartość największą dokładnie w środku między pierwiastkami, czyli dla

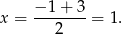
− 1 + 3 x = ---2--- = 1.

Mamy zatem

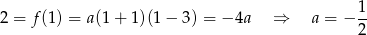
1- 2 = f(1 ) = a(1+ 1)(1− 3) = − 4a ⇒ a = − 2

oraz

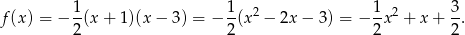
1 1 1 3 f (x) = − -(x + 1 )(x− 3) = − -(x 2 − 2x − 3) = − -x 2 + x + -. 2 2 2 2

Sposób II

Jeżeli parabola będąca wykresem funkcji 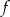f ma przyjmować wartość największą, to jej ramiona muszą być skierowane w dół. Znamy ponadto jej miejsca zerowe, więc możemy obliczyć pierwszą współrzędną jej wierzchołka

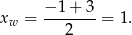
− 1+ 3 xw = ------- = 1. 2

Funkcja 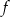f ma więc postać kanoniczną

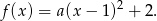
2 f (x) = a(x − 1) + 2.

Współczynnik a obliczamy podstawiając jedno z miejsc zerowych.

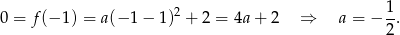
1 0 = f(− 1) = a (−1 − 1 )2 + 2 = 4a+ 2 ⇒ a = − --. 2

Mamy zatem

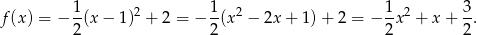
1 1 1 3 f (x) = − --(x− 1)2 + 2 = − -(x 2 − 2x + 1)+ 2 = − -x 2 + x + -. 2 2 2 2

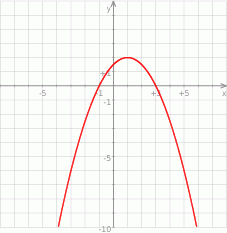
Na koniec wykres funkcji 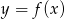y = f (x) .

PIC

 
Odpowiedź: f (x) = − 12x2 + x + 32

Wersja PDF