/Szkoła średnia/Funkcje

Zadanie nr 7385687

Dodaj do ulubionych
Dodaj do rozwiązanych

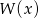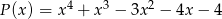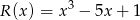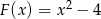Reszta z dzielenia wielomianu W (x) przez wielomian 4 3 2 P (x) = x + x − 3x − 4x − 4 jest wielomianem R(x) = x3 − 5x + 1 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian F (x) = x 2 − 4 .

Rozwiązanie

Szukana reszta jest wielomianem stopnia 1, czyli jest postaci 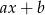ax + b oraz

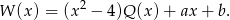
W (x ) = (x2 − 4)Q (x) + ax + b.

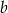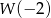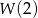Aby wyznaczyć a i b musimy znać wartości W (− 2) i W (2) (w miejscach zerowych wielomianu 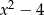x 2 − 4 ). Wartości te możemy wyliczyć z podanego warunku

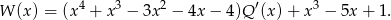
4 3 2 ′ 3 W (x ) = (x + x − 3x − 4x − 4)Q (x)+ x − 5x + 1.

Liczymy

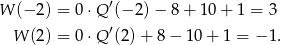
W (− 2) = 0 ⋅Q ′(− 2) − 8 + 10 + 1 = 3 ′ W (2) = 0 ⋅Q (2 )+ 8 − 10 + 1 = − 1.

Możemy teraz wyznaczyć a i b .

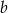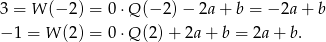
3 = W (− 2) = 0 ⋅Q (− 2) − 2a + b = − 2a + b − 1 = W (2) = 0 ⋅Q (2) + 2a + b = 2a + b.

Dodając te dwie równości stronami mamy 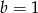b = 1 , stąd a = − 1 .  
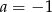Odpowiedź: − x + 1

Wersja PDF