Zadanie nr 7398729
Reszta z dzielenia wielomianu 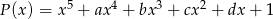 przez dwumian
przez dwumian 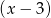 jest równa 1. Wykaż, że jeżeli liczby
jest równa 1. Wykaż, że jeżeli liczby 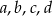 są liczbami całkowitymi to wielomian
są liczbami całkowitymi to wielomian 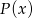 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
Rozwiązanie
Reszta z dzielenia wielomianu 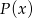 przez
przez 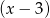 to po prostu
to po prostu 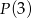 , więc wiemy, że
, więc wiemy, że
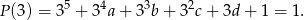
Z drugiej strony, na mocy twierdzenia o wymiernych pierwiastkach wielomianów, jedynymi wymiernymi pierwiastkami wielomianu 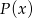 mogą być dzielniki wyrazu wolnego, czyli
mogą być dzielniki wyrazu wolnego, czyli 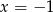 lub
lub 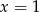 .
.
Gdyby 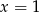 był pierwiastkiem
był pierwiastkiem 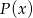 to wtedy
to wtedy
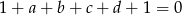
Jeżeli dodamy tę równość od poprzedniej równości na 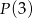 , to otrzymamy
, to otrzymamy
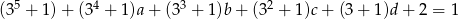
Zauważmy jednak, że z lewej strony mamy same liczby parzyste, co jest sprzeczne z 1-ką z prawej strony.
Podobnie, jeżeli 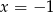 byłby pierwiastkiem to mamy
byłby pierwiastkiem to mamy
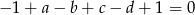
i dodając to do równości na 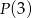 , mamy
, mamy
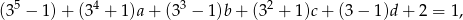
co też jest niemożliwe (lewa strona jest parzysta, a prawa nie).

