/Szkoła średnia/Funkcje

Zadanie nr 7666393

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa jest określona wzorem 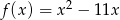2 f(x) = x − 1 1x . Oblicz najmniejszą wartość funkcji 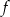f w przedziale ⟨− 6,6⟩ .

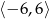Rozwiązanie

Wierzchołek paraboli będącej wykresem funkcji

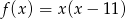
f (x) = x(x − 11 )

znajduje się w środku między pierwiastkami, czyli w

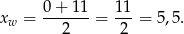
0 + 11 11 xw = -------= ---= 5,5. 2 2

To oznacza, że wierzchołek paraboli znajduje się wewnątrz interesującego nas przedziału.

PIC

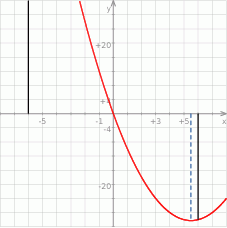
W takim razie najmniejsza wartość funkcji na tym przedziale to

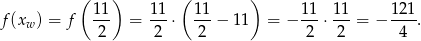
( ) ( ) f (xw ) = f 11- = 11-⋅ 11-− 11 = − 11-⋅ 11-= − 1-21. 2 2 2 2 2 4

 
Odpowiedź: ( ) fmin = f 11 = − 121 2 4

Wersja PDF