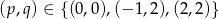/Szkoła średnia/Funkcje

Zadanie nr 7696661

Dodaj do ulubionych
Dodaj do rozwiązanych

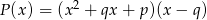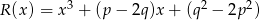Wielomiany 2 P (x) = (x + qx + p)(x − q ) i 3 2 2 R (x) = x + (p − 2q)x + (q − 2p ) są równe. Oblicz 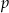p i q .

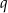Rozwiązanie

Przekształćmy wzór wielomianu 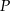P (wymnażamy nawiasy).

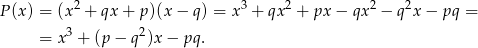
2 3 2 2 2 P (x) = (x + qx + p )(x− q) = x + qx + px − qx − q x− pq = = x3 + (p − q2)x − pq .

Z drugiej strony wiemy, że wielomian ten jest równy 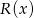R (x) . Dwa wielomiany są równe jeżeli mają takie same współczynniki, więc otrzymujemy układ równań.

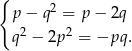
{ p− q2 = p − 2q 2 2 q − 2p = −pq .

Z pierwszego równania mamy

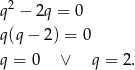
2 q − 2q = 0 q(q− 2) = 0 q = 0 ∨ q = 2.

Jeżeli 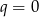q = 0 to drugie równanie przyjmuje postać

− 2p2 = 0 .

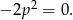
Mamy stąd jedno rozwiązanie 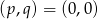(p,q) = (0 ,0) .

Jeżeli natomiast 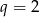q = 2 to drugie równanie przybiera postać

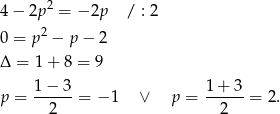
4− 2p2 = − 2p / : 2 0 = p2 − p − 2 Δ = 1+ 8 = 9 p = 1−-3-= − 1 ∨ p = 1-+-3-= 2 . 2 2

Mamy stąd dwa dodatkowe rozwiązania 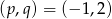(p,q) = (− 1,2) i (p ,q) = (2,2) .  
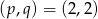Odpowiedź: (p,q) ∈ { (0,0),(− 1,2),(2,2)}

Wersja PDF