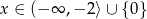Zadanie nr 8786871

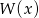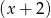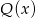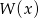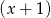W wyniku podzielenia wielomianu W (x) przez (x + 2) otrzymujemy iloraz Q (x) i resztę 0. Jeśli natomiast podzielimy wielomian W (x) przez (x + 1) , to otrzymamy iloraz 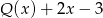Q (x)+ 2x − 3 i resztę 2.

Wyznacz wielomian .
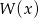Rozwiąż nierówność .

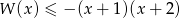Rozwiązanie

Z podanych informacji mamy układ równań
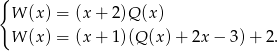
${ W (x ) = (x + 2)Q (x) W (x ) = (x + 1)(Q (x) + 2x − 3) + 2.$

Zatem

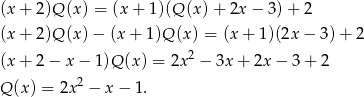
$(x+ 2)Q (x) = (x + 1)(Q (x) + 2x − 3) + 2 (x+ 2)Q (x)− (x+ 1)Q (x) = (x + 1)(2x − 3 )+ 2 (x+ 2− x− 1)Q (x) = 2x2 − 3x + 2x − 3+ 2 Q(x ) = 2x2 − x − 1.$

Stąd

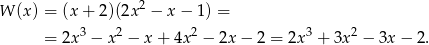
$2 W (x ) = (x + 2)(2x − x − 1) = = 2x3 − x2 − x + 4x2 − 2x − 2 = 2x3 + 3x2 − 3x − 2.$

Odpowiedź: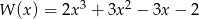
Z poprzedniego podpunktu wiemy, że 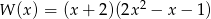. Mamy więc nierówność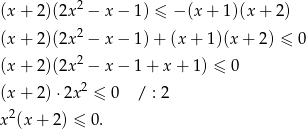
$(x+ 2)(2x2 − x − 1) ≤ − (x + 1)(x + 2) 2 (x+ 2)(2x − x − 1) + (x + 1)(x + 2) ≤ 0 (x+ 2)(2x2 − x − 1 + x + 1) ≤ 0 2 (x+ 2)⋅2x ≤ 0 / : 2 x2(x + 2) ≤ 0.$

Oczywiście 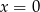spełnia powyższą nierówność, a jeżeli 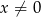to możemy obie strony podzielić przez 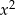i otrzymujemy .
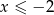Odpowiedź: