Zadanie nr 9474654
Funkcja homograficzna 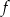 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 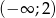 i
i 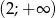 . Zbiór
. Zbiór 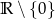 jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
- Znajdź wzór funkcji
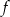 .
. - Naszkicuj wykres funkcji
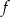 .
. - Uzasadnij, że funkcja
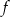 nie jest monotoniczna w zbiorze
nie jest monotoniczna w zbiorze 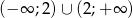 .
.
Rozwiązanie
- Najlepiej jest myśleć o hiperboli będącej wykresem funkcji
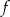 – z podanych informacji wynika, że ma ona asymptoty
– z podanych informacji wynika, że ma ona asymptoty 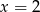 i
i 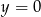 . Funkcja ma zatem wzór postaci
. Funkcja ma zatem wzór postaci 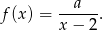
Współczynnik
 wyznaczymy z warunku
wyznaczymy z warunku 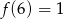 .
. 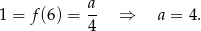
Odpowiedź: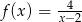
- Wykres funkcji
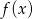 powstaje z wykresu funkcji
powstaje z wykresu funkcji  przez przesunięcie o 2 jednostki w prawo.
przez przesunięcie o 2 jednostki w prawo. 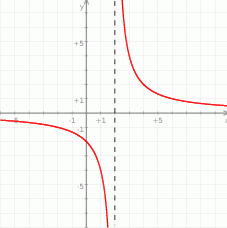
- Aby pokazać, że funkcja nie jest monotoniczna musimy pokazać, że nie jest ani malejąca ani rosnąca. Łatwo znaleźć odpowiednie punkty
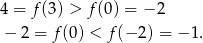
Pierwsza nierówność oznacza, że funkcja nie jest malejąca, druga, że nie jest rosnąca.

