/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 11 kwietnia 2015 Czas pracy: 180 minut
Zadania zamknięte
Styczna do wykresu funkcji 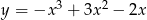 w punkcie
w punkcie 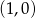 ma równanie
ma równanie
A) 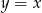 B)
B) 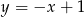 C)
C) 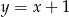 D)
D) 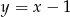
Wskaż wartość parametru 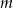 , dla którego prosta
, dla którego prosta 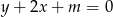 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 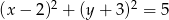
A) 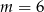 B)
B) 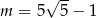 C)
C) 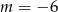 D)
D) 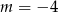
Suma szeregu geometrycznego 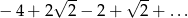 jest równa
jest równa
A) 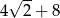 B)
B) 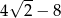 C)
C) 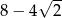 D)
D) 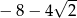
Która z poniższych liczb jest ujemna?
A) 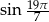 B)
B) 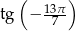 C)
C) 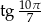 D)
D) 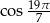
Funkcja 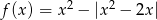 określona dla wszystkich liczb rzeczywistych
określona dla wszystkich liczb rzeczywistych
A) ma trzy miejsca zerowe.
B) jest rosnąca.
C) ma jedno minimum lokalne.
D) nie ma ekstremów lokalnych.
Zadania otwarte
Wiedząc, że 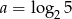 , oblicz
, oblicz 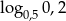 .
.
Oblicz granicę 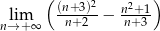 .
.
Funkcja 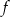 jest określona wzorem
jest określona wzorem 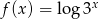 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 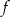 w punkcie
w punkcie 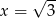
Rozwiąż równanie 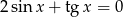 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 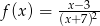 .
.
Wyznacz liczbę 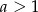 , która spełnia równanie
, która spełnia równanie 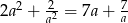 .
.
Promienie okręgów 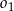 i
i 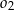 są równe odpowiednio
są równe odpowiednio 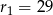 i
i 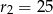 , a odległość między środkami tych okręgów jest równa 36. Oblicz długość odcinka łączącego punkty wspólne okręgów
, a odległość między środkami tych okręgów jest równa 36. Oblicz długość odcinka łączącego punkty wspólne okręgów 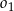 i
i 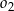 .
.
Rzucamy sześcienną kostką do gry tak długo, aż otrzymamy co najmniej dwie nieparzyste liczby oczek, albo 10 parzystych liczb oczek. Oblicz prawdopodobieństwo, że w przeprowadzonym doświadczeniu otrzymaliśmy liczbę oczek równą 5, przy założeniu, że otrzymaliśmy tylko jedną nieparzystą liczbę oczek.
Wykaż, że jeżeli 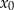 jest rozwiązaniem równania
jest rozwiązaniem równania 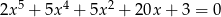 , to
, to 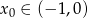 .
.
Na bokach 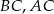 i
i 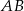 trójkąta
trójkąta 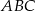 wybrano odpowiednio punkty
wybrano odpowiednio punkty 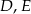 i
i 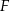 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 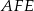 i
i 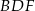 są styczne, to punkt
są styczne, to punkt 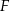 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 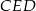 .
.
Dwa boki trójkąta równoramiennego są zawarte w osiach układu współrzędnych, a prosta zawierająca trzeci bok tego trójkąta jest styczna do paraboli o równaniu 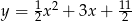 . Oblicz pole tego trójkąta. Rozważ wszystkie możliwe przypadki.
. Oblicz pole tego trójkąta. Rozważ wszystkie możliwe przypadki.
Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, pod kątem  do dolnej podstawy. Pole otrzymanego przekroju wynosi
do dolnej podstawy. Pole otrzymanego przekroju wynosi 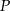 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Oblicz prawdopodobieństwo, że w czterech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 5.

