/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 11 kwietnia 2015 Czas pracy: 180 minut
Dane są punkty 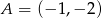 i
i 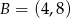 . Wyznacz te punkty prostej
. Wyznacz te punkty prostej 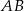 , dla których różnica odległości od punktu
, dla których różnica odległości od punktu 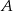 i odległości od punktu
i odległości od punktu 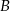 jest większa niż odległość od punktu
jest większa niż odległość od punktu 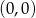 .
.
Ciąg 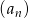 jest określony wzorem
jest określony wzorem 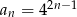 , gdzie
, gdzie 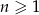 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 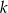 , dla których iloczyn
, dla których iloczyn 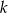 początkowych wyrazów ciągu
początkowych wyrazów ciągu 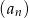 jest równy
jest równy 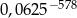 .
.
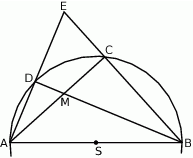
Na okręgu o środku 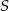 wybrano punkty
wybrano punkty 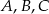 i
i 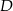 w ten sposób, że prosta
w ten sposób, że prosta 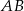 zawiera punkt
zawiera punkt 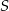 , a proste
, a proste 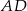 i
i 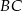 przecinają się w punkcie
przecinają się w punkcie 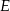 . Punkt
. Punkt 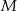 jest punktem wspólnym prostych
jest punktem wspólnym prostych 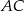 i
i 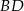 . Wykaż, że proste
. Wykaż, że proste 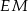 i
i 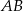 są prostopadłe.
są prostopadłe.
Dane są dwa nieskończone ciągi 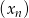 i
i 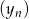 takie, że dla każdego
takie, że dla każdego 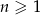 , punkt o współrzędnych
, punkt o współrzędnych 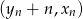 jest środkiem ciężkości trójkąta o wierzchołkach
jest środkiem ciężkości trójkąta o wierzchołkach 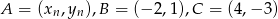 . Wyznacz wzory ciągów
. Wyznacz wzory ciągów 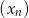 i
i 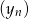 .
.
Wykaż, że jeżeli 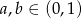 to prawdziwa jest nierówność
to prawdziwa jest nierówność
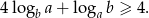
Wyznacz wszystkie wartości parametru 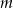 , dla których równanie
, dla których równanie 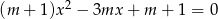 ma dwa różne pierwiastki takie, że ich suma jest nie większa niż 2,5.
ma dwa różne pierwiastki takie, że ich suma jest nie większa niż 2,5.
Wyznacz wszystkie wartości parametru 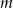 , dla których równanie
, dla których równanie
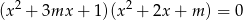
ma cztery różne pierwiastki, których suma sześcianów jest równa 4.
Okrąg wpisany w trójkąt prostokątny 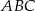 o bokach długości
o bokach długości 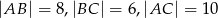 jest styczny do boków
jest styczny do boków 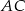 i
i 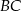 w punktach
w punktach 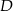 i
i 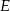 . Proste
. Proste 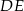 i
i 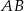 przecinają się punkcie
przecinają się punkcie 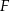 . Oblicz pole trójkąta
. Oblicz pole trójkąta 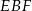 .
.
Rozwiąż równanie 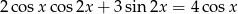 .
.
Suma długości krawędzi graniastosłupa prawidłowego czworokątnego jest równa 16. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?
Ze zbioru 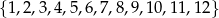 losujemy podzbiór trójelementowy. Jakie jest prawdopodobieństwo, że iloczyn liczb będących elementami wylosowanego podzbioru jest liczbą parzystą?
losujemy podzbiór trójelementowy. Jakie jest prawdopodobieństwo, że iloczyn liczb będących elementami wylosowanego podzbioru jest liczbą parzystą?

