/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna
Lubelska próba przed maturą
z matematyki poziom rozszerzony 25 lutego 2015 Czas pracy: 180 minut
Zadania zamknięte
Liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 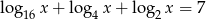 . Zatem
. Zatem
A) 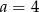 B)
B) 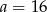 C)
C) 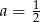 D)
D) 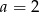
Wyrażenie 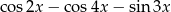 jest równe
jest równe
A) 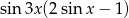
B) 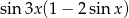
C) 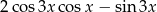
D) 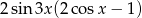
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a różnica tego ciągu jest równa 3. Suma 100 początkowych wyrazów tego ciągu o numerach parzystych jest równa
A) 15100 B) 30500 C) 30200 D) 61000
Funkcja 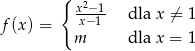 jest funkcją ciągłą. Wtedy
jest funkcją ciągłą. Wtedy
A) 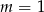 B)
B) 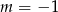 C) nie istnieje takie
C) nie istnieje takie 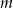 D)
D) 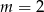
Ile rozwiązań ma układ równań 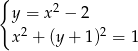 ?
?
A) 0 B) 1 C) 2 D) 3
Zadania otwarte
W pudełku jest 7 kul białych i 3 czarne. Doświadczenie polega na wylosowaniu 3 kul. Jakie jest prawdopodobieństwo wylosowania co najwyżej dwóch kul białych?
Oblicz granicę 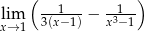 .
.
Oblicz pochodną funkcji 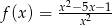 w punkcie
w punkcie 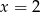 .
.
Wykaż, że jeżeli 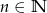 , to liczba postaci
, to liczba postaci 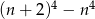 jest podzielna przez 16.
jest podzielna przez 16.
Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.
W trapez prostokątny wpisano okrąg o promieniu  . Najkrótszy bok tego trapezu ma długość
. Najkrótszy bok tego trapezu ma długość 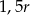 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Wyznacz resztę z dzielenia wielomianu 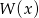 przez wielomian
przez wielomian 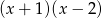 wiedząc, że
wiedząc, że 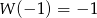 i
i 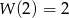 .
.
Rzucamy dwukrotnie kostką do gry. Jakie jest prawdopodobieństwo, że suma wyrzuconych oczek jest większa niż 9, jeżeli wiadomo, że dokładnie jeden raz wypadło 6 oczek?
Wyznacz wszystkie wartości parametru 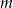 , dla których równanie
, dla których równanie 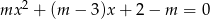 ma dwa rozwiązania dodatnie.
ma dwa rozwiązania dodatnie.
W zbieżnym nieskończonym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a różnica między trzecim i piątym wyrazem jest równa 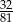 . Jaka jest suma wyrazów tego ciągu?
. Jaka jest suma wyrazów tego ciągu?
Punkt 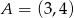 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 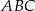 , o kącie prostym
, o kącie prostym 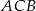 , a
, a 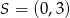 jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że
jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że 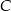 należy do ujemnej części osi
należy do ujemnej części osi 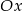 .
.
Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego jest równa 36. Jakie są wymiary graniastosłupa o największej objętości?

