/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa II 3 czerwca 2014 Czas pracy: 170 minut
Zadania zamknięte
Liczba 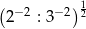 jest równa
jest równa
A)  B)
B)  C)
C) 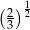 D)
D) 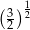
Wiadomo, że liczba 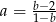 dla
dla 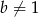 . Zatem
. Zatem
A) 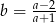 B)
B) 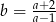 C)
C) 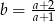 D)
D) 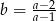
Liczbą odwrotną do liczby 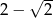 jest liczba
jest liczba
A) 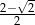 B)
B) 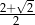 C)
C) 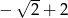 D)
D) 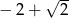
Liczby  i
i 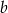 są dodatnie oraz 20% liczby
są dodatnie oraz 20% liczby  jest równe 25% liczby
jest równe 25% liczby 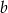 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 110% liczby 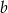 B) 120% liczby
B) 120% liczby 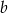 C) 115% liczby
C) 115% liczby 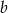 D) 125% liczby
D) 125% liczby 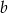
Liczba 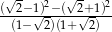 jest równa:
jest równa:
A) 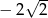 B)
B) 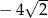 C)
C) 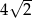 D)
D) 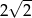
Trójkąt 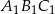 o polu
o polu 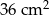 jest podobny do trójkąta
jest podobny do trójkąta 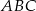 o polu
o polu 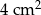 . Skala podobieństwa trójkąta
. Skala podobieństwa trójkąta 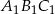 do trójkąta
do trójkąta 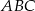 jest równa
jest równa
A) 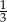 B) 3 C) 12 D) 9
B) 3 C) 12 D) 9
Środkowa w trójkącie prostokątnym poprowadzona z wierzchołka kąta prostego ma długość 1. Zatem pole koła opisanego na tym trójkącie wynosi
A) 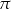 B)
B) 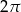 C)
C) 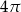 D)
D) 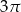
Liczba 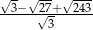 jest równa
jest równa
A) 5 B) 6 C) 8 D) 7
Jeżeli różnica między liczbą  i liczbą
i liczbą 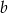 wynosi 5, a różnica między kwadratami tych liczb jest równa 75, to suma tych liczb jest równa
wynosi 5, a różnica między kwadratami tych liczb jest równa 75, to suma tych liczb jest równa
A) 15 B) 35 C) 25 D) 45
Długości boków trójkąta wynoszą 2 i 8, zaś kąt między nimi zawarty ma miarę 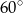 . Pole tego trójkąta wynosi
. Pole tego trójkąta wynosi
A) 8 B) 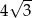 C) 4 D)
C) 4 D) 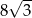
Dla jakiego argumentu funkcja 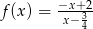 przyjmuje wartość 4?
przyjmuje wartość 4?
A) 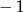 B) 1 C) 0 D) 2
B) 1 C) 0 D) 2
Prostokąt o bokach 10 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 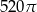 B)
B) 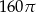 C)
C) 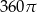 D)
D) 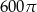
Pole powierzchni bocznej graniastosłupa prawidłowego trójkątnego o wysokości 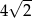 i długości krawędzi przy podstawie równej 4 wynosi
i długości krawędzi przy podstawie równej 4 wynosi
A) 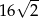 B)
B) 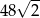 C)
C) 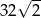 D)
D) 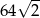
Pole wycinka koła (zacieniowana część na rysunku) jest równe
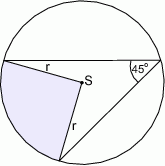
A) 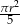 B)
B) 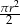 C)
C) 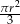 D)
D) 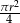
Rozwiązaniem układu nierówności 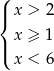 jest następujący przedział liczb
jest następujący przedział liczb
A) 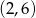 B)
B) 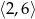 C)
C) 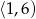 D)
D) 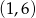
Kąt między ramionami trójkąta równoramiennego ma miarę 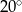 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 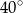 B)
B) 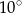 C)
C) 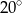 D)
D) 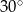
Ile liczb całkowitych należy do zbioru rozwiązań układu nierówności 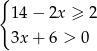 ?
?
A) 5 B) 6 C) 8 D) 7
Bezrobocie w pewnym kraju wynosi 10%. Które z poniższych zdań jest fałszywe?
A) Jeżeli bezrobocie wzrośnie o 5 punktów procentowych, to będzie wynosiło 15%.
B) Jeżeli bezrobocie zmaleje o 3 punkty procentowe, to będzie wynosiło 7%.
C) Jeżeli bezrobocie wzrośnie o 10%, to będzie wynosiło 11%.
D) Jeżeli bezrobocie spadnie o 5%, to będzie wynosiło 5%.
Jeśli wiadomo, że 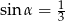 i
i  jest kątem ostrym, to prawdą jest, że
jest kątem ostrym, to prawdą jest, że
A) 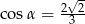 B)
B) 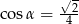 C)
C) 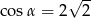 D)
D) 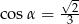
Liczbą, która nie należy do zbioru wartości funkcji 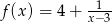 jest
jest
A) 3 B) 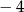 C) 4 D)
C) 4 D) 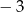
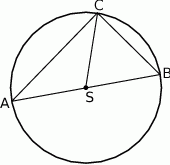
Na rysunku poniżej punkt 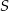 jest środkiem okręgu i miara kąt
jest środkiem okręgu i miara kąt 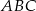 wynosi
wynosi 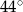 . Ile stopni ma kąt
. Ile stopni ma kąt 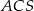 ?
?
A) 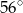 B)
B) 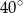 C)
C) 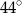 D)
D) 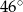
Dziedziną funkcji 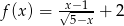 jest zbiór
jest zbiór
A) 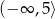 B)
B) 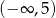 C)
C) 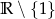 D)
D) 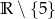
Jaką miarę ma kąt wpisany oparty na  łuku okręgu?
łuku okręgu?
A) 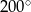 B)
B) 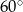 C)
C) 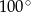 D)
D) 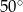
Zadania otwarte
Rozwiąż równanie 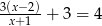 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 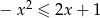 .
.
Z punktu 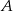 leżącego na okręgu poprowadź cięciwę
leżącego na okręgu poprowadź cięciwę 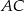 o długości równej promieniowi okręgu oraz średnicę
o długości równej promieniowi okręgu oraz średnicę 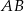 . Wyznacz miary kątów wewnętrznych trójkąta
. Wyznacz miary kątów wewnętrznych trójkąta 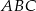 .
.
W trójkąt równoramienny o podstawie 24 cm i wysokości 5 cm wpisano okrąg. Oblicz promień tego okręgu.
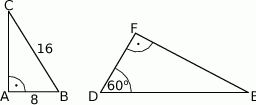
Uzasadnij, że trójkąty prostokątne 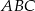 i
i 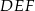 (patrz rysunek) są podobne.
(patrz rysunek) są podobne.
Suma cyfr pewnej liczby dwucyfrowej wynosi 14. Jeśli do tej liczby dodamy 18, to otrzymamy liczbę utworzoną z tych samych cyfr, ale napisanych w odwrotnej kolejności. Wyznacz tę liczbę.
W trapezie, którego podstawy mają długości 12 cm i 6 cm, miary kątów przy dłuższej podstawie wynoszą 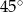 i
i 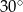 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Ile trzeba zmieszać roztworu wodnego soli kuchennej o stężeniu 20% z roztworem o stężeniu 8% żeby otrzymać 12 kg roztworu o stężeniu 13%?
Z wykresu funkcji 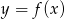 przedstawionego na rysunku odczytaj:
przedstawionego na rysunku odczytaj:
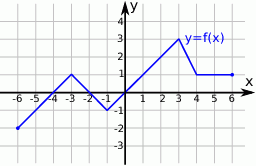
- dziedzinę i zbiór wartości funkcji;
- jej miejsca zerowe;
- maksymalne przedziały, w których funkcja jest malejąca;
- dla jakich argumentów funkcja przyjmuje wartość równą 2;
- zbiór rozwiązań nierówności
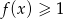 .
.

