/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/CKE, OKE, CEN

Lubelska próba przed maturą
z matematyki poziom rozszerzony
(technikum) 25 lutego 2015 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Wyznacz dziedzinę funkcji 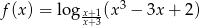f(x) = log x+1(x3 − 3x + 2) x+3 .

Zadanie 2
(5 pkt)

Dla jakich wartości parametru 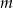m suma kwadratów dwóch różnych pierwiastków równania 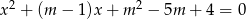x 2 + (m − 1)x + m 2 − 5m + 4 = 0 przyjmuje wartość największą. Wyznacz tę wartość.

Zadanie 3
(4 pkt)

Rozwiąż równanie 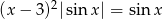(x − 3)2|sin x| = sinx w zbiorze ⟨0,2π ⟩ .

Zadanie 4
(5 pkt)

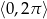Wysokość trójkąta 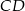CD ma długość 4 i dzieli bok 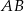AB na odcinki, z których krótszy 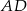AD ma długość 2, a kąt 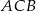ACB na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku 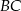BC tego trójkąta.

Zadanie 5
(2 pkt)

Wykaż, że jeśli 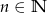n ∈ N , to liczba 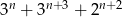n n+ 3 n+2 3 + 3 + 2 jest podzielna przez 4.

Zadanie 6
(5 pkt)

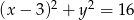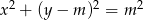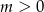Dane są dwa okręgi o równaniach 2 2 (x− 3) + y = 16 i 2 2 2 x + (y − m ) = m , m > 0 . Wyznacz wszystkie wartości parametru 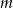m , dla których te okręgi mają jeden punkt wspólny.

Zadanie 7
(5 pkt)

Kierowca obliczył, że trasę 220 km pokona w czasie 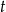t , jeśli będzie jechał ze średnią prędkością v . Wyjechał o 20 minut później niż zamierzał, więc aby dojechać na zaplanowaną godzinę, musiał zwiększyć prędkość o 5 km/h. Oblicz średnią prędkość z jaką planował jechać kierowca.

Zadanie 8
(3 pkt)

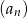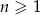Niech ciąg (an) , dla n ≥ 1 , będzie resztą z dzielenia wielomianu 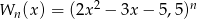W (x) = (2x 2 − 3x− 5,5)n n przez dwumian 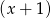(x+ 1) . Oblicz sumę dziesięciu początkowych wyrazów ciągu (an) .

Zadanie 9
(5 pkt)

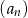Kąt ostry równoległoboku ma miarę 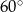∘ 60 . Stosunek kwadratów długości przekątnych jest równy 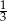1 3 . Wykaż, że ten równoległobok jest rombem.

Zadanie 10
(5 pkt)

W urnie znajduje się dwa razy więcej kul białych niż czarnych. Losujemy z urny jednocześnie dwie kule. Prawdopodobieństwo wylosowania obu kul białych jest równe 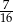176 . Oblicz prawdopodobieństwo wylosowania kul różnych kolorów.

Zadanie 11
(6 pkt)

Krawędź sześcianu ma długość a . Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.

Arkusz Wersja PDF
Rozwiązania