/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki poziom rozszerzony Grudzień 2013 Czas pracy: 180 minut
Zadania zamknięte
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 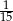 B)
B)  C)
C) 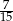 D)
D) 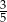
Dany jest nieskończony ciąg geometryczny 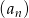 określony wzorem
określony wzorem 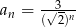 dla
dla 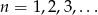 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A) 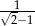 B)
B) 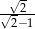 C)
C) 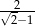 D)
D) 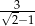
Liczba 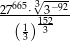 jest równa
jest równa
A) 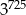 B)
B) 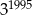 C)
C) 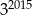 D)
D) 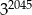
Okrąg 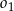 ma równanie
ma równanie 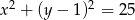 , a okrąg
, a okrąg  ma równanie
ma równanie 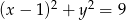 . Określ wzajemne położenie tych okręgów.
. Określ wzajemne położenie tych okręgów.
A) Te okręgi przecinają się w dwóch punktach.
B) Te okręgi są styczne.
C) Te okręgi nie mają punktów wspólnych oraz okrąg  leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 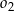 .
.
D) Te okręgi nie mają punktów wspólnych oraz okrąg 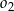 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 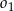 .
.
Dla każdego  suma
suma 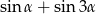 jest równa
jest równa
A) 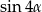 B)
B) 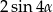 C)
C) 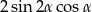 D)
D) 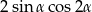
Zadania otwarte
Wyznacz najmniejszą liczbę całkowitą  spełniającą równanie
spełniającą równanie
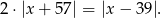
Oblicz granicę ciągu 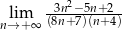 .
.
Dana jest funkcja 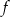 określona wzorem
określona wzorem 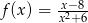 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej  . Oblicz wartość pochodnej tej funkcji w punkcie
. Oblicz wartość pochodnej tej funkcji w punkcie 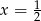 .
.
Oblicz 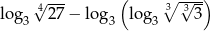 .
.
Punkty 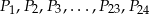 dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt 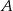 jest punktem przecięcia cięciw
jest punktem przecięcia cięciw 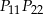 i
i 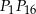 .
.
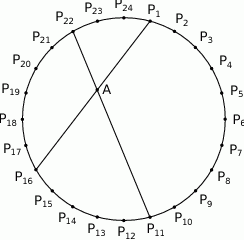
Udowodnij, że 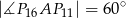 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 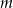 prawdziwa jest nierówność
prawdziwa jest nierówność 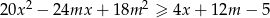 .
.
Janek przeprowadza doświadczenie losowe, w którym jako wynik może otrzymać jedną z liczb: 0, 1, 2, 3, 4, 5, 6. Prawdopodobieństwo 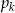 otrzymania liczby
otrzymania liczby 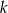 jest dane wzorem:
jest dane wzorem: 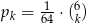 . Rozważamy dwa zdarzenia:
. Rozważamy dwa zdarzenia:
– zdarzenie 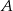 polegające na otrzymaniu liczby ze zbioru
polegające na otrzymaniu liczby ze zbioru 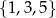 ,
,
– zdarzenie 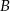 polegające na otrzymaniu liczby ze zbioru
polegające na otrzymaniu liczby ze zbioru 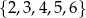 .
.
Oblicz prawdopodobieństwo warunkowe 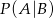
Wyznacz wszystkie wartości parametru 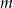 , dla których prosta o równaniu
, dla których prosta o równaniu 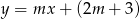 ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie
ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie 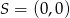 i promieniu
i promieniu 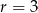 .
.
Dana jest parabola o równaniu 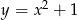 i leżący na niej punkt
i leżący na niej punkt 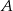 o współrzędnej
o współrzędnej  równej 3. Wyznacz równanie stycznej do tej paraboli w punkcie
równej 3. Wyznacz równanie stycznej do tej paraboli w punkcie 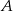 .
.
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość  . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę
. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę 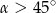 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
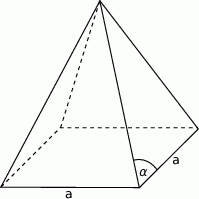
Punkty 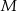 i
i 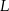 leżą odpowiednio na bokach
leżą odpowiednio na bokach 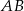 i
i 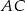 trójkąta
trójkąta 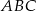 , przy czym zachodzą równości
, przy czym zachodzą równości 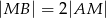 oraz
oraz 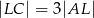 . Punkt
. Punkt 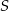 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 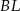 i
i 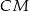 . Punkt
. Punkt 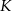 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 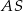 z odcinkiem
z odcinkiem 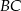 (zobacz rysunek).
(zobacz rysunek).
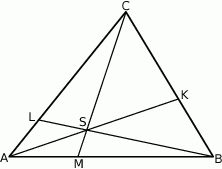
Pole trójkąta 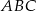 jest równe 660. Oblicz pola trójkątów:
jest równe 660. Oblicz pola trójkątów: 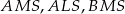 i
i 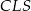 .
.
Oblicz, ile jest stucyfrowych liczb naturalnych o sumie cyfr równej 4.
Dany jest prostokątny arkusz kartonu o długości 80 cm i szerokości 50 cm. W czterech rogach tego arkusza wycięto kwadratowe naroża (zobacz rysunek).

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długość boku wyciętych kwadratowych naroży, dla której objętość otrzymanego pudełka jest największa. Oblicz tę objętość.

