/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki poziom podstawowy 16 grudnia 2014 Czas pracy: 170 minut
Zadania zamknięte
Liczba 0,6 jest jednym z przybliżeń liczby  . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 0,025% B) 2,5% C) 0,04% D) 4%
Dany jest okrąg o środku 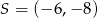 i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi 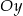 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 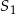 . Odległość między punktami
. Odległość między punktami 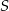 i
i 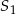 jest równa
jest równa
A) 12 B) 16 C) 2014 D) 4028
Rozwiązaniami równania 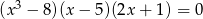 są liczby
są liczby
A) 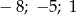 B)
B) 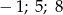 C)
C) 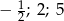 D)
D) 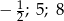
Cena towaru została podwyższona o 30%, a po pewnym czasie nową, wyższą cenę ponownie podwyższono, tym razem o 10%. W rezultacie obu podwyżek wyjściowa cena towaru zwiększyła się o
A) 15% B) 20% C) 40% D) 43%
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 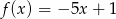 oraz
oraz 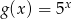 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 3 B) 2 C) 1 D) 0
Wyrażenie 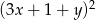 jest równe
jest równe
A) 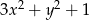
B) 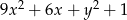
C) 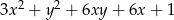
D) 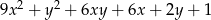
Połowa sumy 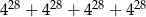 jest równa
jest równa
A) 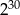 B)
B) 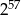 C)
C) 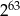 D)
D) 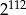
Równania 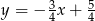 oraz
oraz 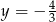 opisują dwie proste
opisują dwie proste
A) przecinające się pod kątem o mierze 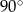 .
.
B) pokrywające się
C) przecinające się pod kątem różnym od 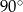 .
.
D) równoległe i różne.
Na płaszczyźnie dane są punkty: 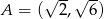 ,
, 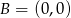 i
i 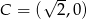 . Kąt
. Kąt 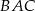 jest równy
jest równy
A) 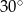 B)
B) 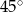 C)
C) 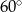 D)
D) 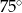
Funkcja 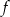 , określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie
, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie  ostatnią cyfrę jej kwadratu. Zbiór wartości funkcji
ostatnią cyfrę jej kwadratu. Zbiór wartości funkcji 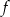 zawiera dokładnie
zawiera dokładnie
A) 5 elementów. B) 6 elementów. C) 9 elementów. D) 10 elementów.
Ekipa złożona z 25 pracowników wymieniła tory kolejowe na pewnym odcinku w ciągu 156 dni. Jeśli wymianę torów kolejowych na kolejnym odcinku o tej samej długości trzeba przeprowadzić w ciągu 100 dni, to, przy założeniu takiej samej wydajności, należy zatrudnić do pracy o
A) 14 osób więcej. B) 17 osób więcej. C) 25 osób więcej. D) 39 osób więcej.
Z sześcianu 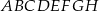 o krawędzi długości
o krawędzi długości  odcięto ostrosłup
odcięto ostrosłup 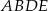 (zobacz rysunek).
(zobacz rysunek).
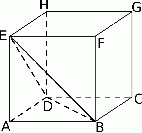
Ile razy objętość tego ostrosłupa jest mniejsza od objętości pozostałej części sześcianu?
A) 2 razy. B) 3 razy. C) 4 razy. D) 5 razy.
W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie 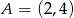 , która jest wykresem funkcji kwadratowej
, która jest wykresem funkcji kwadratowej 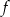 .
.
Funkcja  może być opisana wzorem
może być opisana wzorem
A) 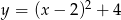 B)
B) 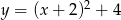 C)
C) 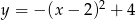 D)
D) 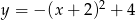
Punkty 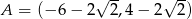 ,
, 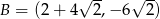 ,
, 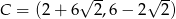 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 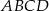 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 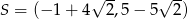
B) 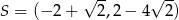
C) 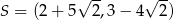
D) 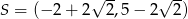
Liczba 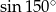 jest równa liczbie
jest równa liczbie
A) 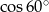 B)
B) 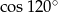 C)
C) 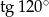 D)
D) 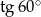
Na ścianie kamienicy zaprojektowano mural utworzony z szeregu trójkątów równobocznych różnej wielkości. Najmniejszy trójkąt ma bok długości 1 m, a bok każdego z następnych trójkątów jest o 10 cm dłuższy niż bok poprzedzającego go trójkąta. Ostatni trójkąt ma bok długości 5,9 m. Ile trójkątów przedstawia mural?
A) 49 B) 50 C) 59 D) 60
Dany jest trójkąt równoramienny, w którym ramię o długości 20 tworzy z podstawą kąt 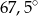 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 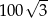 B)
B) 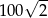 C)
C) 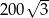 D)
D) 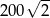
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
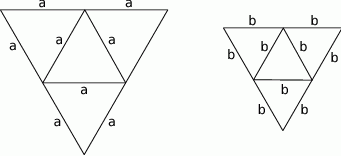
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 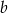 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 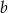 ?
?
A) 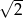 B) 2 C)
B) 2 C) 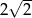 D) 4
D) 4
Na okręgu o środku 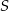 leżą punkty
leżą punkty 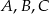 i
i 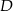 . Odcinek
. Odcinek 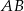 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 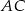 jest równy
jest równy 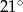 (zobacz rysunek).
(zobacz rysunek).
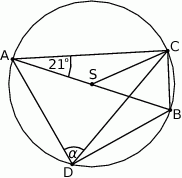
Kąt  między cięciwami
między cięciwami 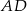 i
i 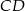 jest równy
jest równy
A) 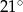 B)
B) 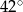 C)
C) 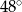 D)
D) 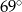
Średnia arytmetyczna zestawu danych: 3, 8, 3, 11, 3, 10, 3,  jest równa 6. Mediana tego zestawu jest równa
jest równa 6. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
Dany jest ciąg geometryczny 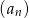 , w którym
, w którym 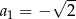 ,
, 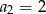 ,
, 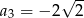 . Dziesiąty wyraz tego ciągu, czyli
. Dziesiąty wyraz tego ciągu, czyli 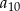 , jest równy
, jest równy
A) 32 B) 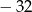 C)
C) 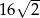 D)
D) 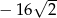
Ciąg 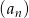 jest określony wzorem
jest określony wzorem 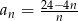 dla
dla 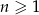 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
A) 7 B) 6 C) 5 D) 4
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Niech 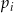 oznacza prawdopodobieństwo wyrzucenia
oznacza prawdopodobieństwo wyrzucenia 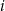 oczek w
oczek w 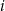 -tym rzucie. Wtedy
-tym rzucie. Wtedy
A) 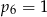 B)
B) 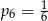 C)
C) 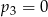 D)
D) 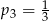
Wskaż liczbę, która spełnia równanie 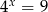 .
.
A) 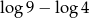 B)
B) 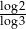 C)
C) 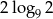 D)
D) 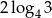
Zadania otwarte
Rozwiąż nierówność: 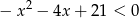 .
.
Uzasadnij, że żadna liczba całkowita nie jest rozwiązaniem równania 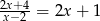 .
.
Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po  okresach rozpadu połowicznego wyraża się wzorem
okresach rozpadu połowicznego wyraża się wzorem 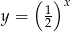 .
.
W przypadku izotopu jodu 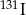 czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g
czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g 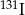 nie więcej niż 0,125 g tego pierwiastka.
nie więcej niż 0,125 g tego pierwiastka.
Uzasadnij, że jeżeli liczba całkowita nie dzieli się przez 3, to jej kwadrat przy dzieleniu przez 3 daje resztę 1.
Wartość prędkości średniej obliczamy jako iloraz drogi i czasu, w którym ta droga została przebyta. Samochód przejechał z miejscowości 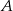 do miejscowości
do miejscowości 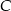 przez miejscowość
przez miejscowość 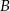 , która znajduje się w połowie drogi z
, która znajduje się w połowie drogi z 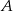 do
do 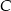 . Wartość prędkości średniej samochodu na trasie z
. Wartość prędkości średniej samochodu na trasie z 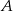 do
do 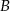 była równa 40 km/h, a na trasie z
była równa 40 km/h, a na trasie z 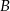 do
do 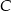 – 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z
– 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z 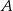 do
do 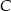 .
.
Zakupiono 16 biletów do teatru, w tym 10 biletów na miejsca od 1. do 10. w pierwszym rzędzie i 6 biletów na miejsca od 11. do 16. w szesnastym rzędzie. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że 2 wylosowane bilety, spośród szesnastu, będą biletami na sąsiadujące miejsca?
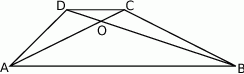
W trapezie 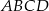 (
(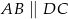 ) przekątne
) przekątne 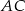 i
i 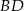 przecinają się w punkcie
przecinają się w punkcie 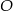 takim, że
takim, że 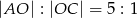 . Pole trójkąta
. Pole trójkąta 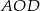 jest równe 10. Uzasadnij, że pole trapezu
jest równe 10. Uzasadnij, że pole trapezu 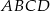 jest równe 72.
jest równe 72.
Punkty 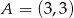 i
i 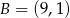 są wierzchołkami trójkąta
są wierzchołkami trójkąta 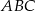 , a punkt
, a punkt 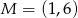 jest środkiem boku
jest środkiem boku 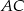 . Oblicz współrzędne punktu przecięcia prostej
. Oblicz współrzędne punktu przecięcia prostej 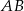 z wysokością tego trójkąta, poprowadzoną z wierzchołka
z wysokością tego trójkąta, poprowadzoną z wierzchołka 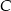 .
.
Tworząca stożka ma długość 17, a wysokość stożka jest krótsza od średnicy jego podstawy o 22. Oblicz pole powierzchni całkowitej i objętość tego stożka.

