/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 21 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczbę 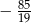 zaokrąglamy do najbliższej liczby całkowitej. Błąd bezwzględny tego przybliżenia jest równy
zaokrąglamy do najbliższej liczby całkowitej. Błąd bezwzględny tego przybliżenia jest równy
A) 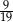 B)
B) 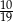 C)
C) 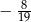 D)
D) 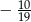
Punkty 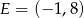 i
i 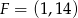 to środki boków, odpowiednio
to środki boków, odpowiednio 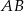 i
i 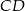 kwadratu
kwadratu 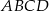 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 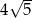 B) 10 C)
B) 10 C) 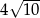 D) 20
D) 20
Wartość wyrażenia 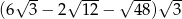 jest równa:
jest równa:
A) 6 B) 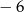 C)
C) 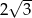 D)
D) 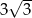
Suma rozwiązań równania  jest równa
jest równa
A) 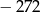 B)
B) 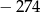 C)
C) 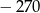 D)
D) 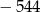
Funkcja wykładnicza określona wzorem 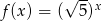 przyjmuje wartość 2 dla argumentu
przyjmuje wartość 2 dla argumentu
A) 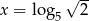 B)
B) 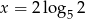 C)
C) 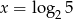 D)
D) 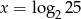
Wyrażenie 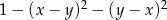 jest równe
jest równe
A) 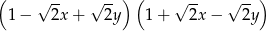
B) 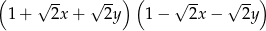
C) 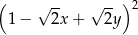
D) 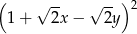
Trzecia część sumy 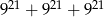 jest równa
jest równa
A) 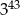 B)
B) 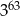 C)
C) 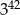 D)
D) 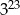
Pole trójkąta wyznaczonego przez wykresy funkcji 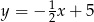 i
i 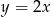 oraz oś
oraz oś 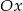 jest równe
jest równe
A) 20 B) 10 C) 32 D) 40
W loterii fantowej jest 9 razy więcej losów przegrywających niż wygrywających. Ile procent wszystkich losów w tej loterii stanowią losy wygrywające?
A) 1% B) 11% C) 10% D) 90%
Okrąg wpisany w trójkąt równoboczny ma promień równy 8. Wysokość tego trójkąta jest równa
A) 12 B) 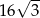 C)
C) 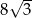 D) 24
D) 24
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem 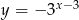 , należy punkt
, należy punkt
A) 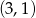 B)
B) 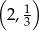 C)
C) 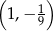 D)
D) 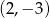
Rysunek przedstawia ostrosłup prawidłowy czworokątny 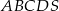 .
.
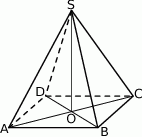
Kątem między krawędzią boczną a wysokością tego ostrosłupa jest kąt
A) 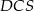 B)
B) 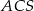 C)
C) 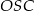 D)
D) 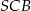
Wskaż równanie paraboli, której osią symetrii jest prosta 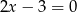 .
.
A) 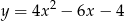
B) 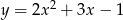
C) 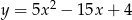
D) 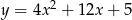
Punkty 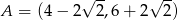 ,
, 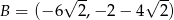 ,
, 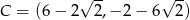 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 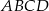 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 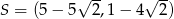
B) 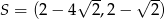
C) 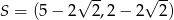
D) 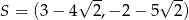
Jeżeli  jest kątem wewnętrznym trójkąta
jest kątem wewnętrznym trójkąta 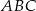 i
i 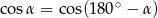 , to trójkąt
, to trójkąt 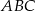 jest trójkątem
jest trójkątem
A) ostrokątnym B) prostokątnym C) rozwartokątnym D) równobocznym
Na ścianie kamienicy zaprojektowano mural utworzony z szeregu trójkątów równobocznych różnej wielkości. Najmniejszy trójkąt ma bok długości 1 m, a bok każdego z następnych trójkątów jest o 15 cm dłuższy niż bok poprzedzającego go trójkąta. Ostatni trójkąt ma bok długości 6,4 m. Ile trójkątów przedstawia mural?
A) 35 B) 36 C) 37 D) 40
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
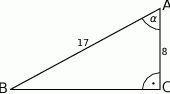
A) 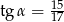 B)
B) 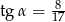 C)
C) 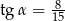 D)
D) 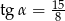
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
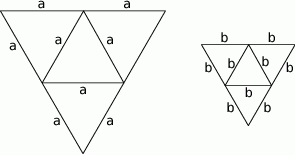
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 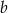 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 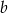 ?
?
A) 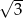 B)
B) 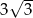 C) 3 D) 9
C) 3 D) 9
Punkt 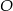 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
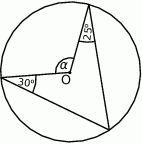
A) 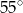 B)
B) 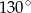 C)
C) 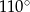 D)
D) 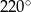
Na przyjęciu spotkało się jedenaście osób i każda osoba uścisnęła dłoń każdej innej osobie. Liczba wszystkich uścisków dłoni była równa
A) 21 B) 55 C) 121 D) 110
W ciągu geometrycznym 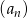 dane są
dane są 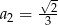 i
i 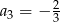 . Wtedy wyraz
. Wtedy wyraz 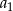 jest równy
jest równy
A) 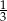 B)
B) 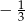 C)
C) 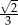 D)
D) 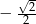
Ciąg 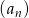 jest określony wzorem
jest określony wzorem 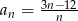 dla
dla 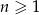 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
A) 6 B) 4 C) 3 D) 2
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Niech 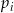 oznacza prawdopodobieństwo wyrzucenia mniej niż
oznacza prawdopodobieństwo wyrzucenia mniej niż 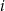 oczek w
oczek w 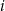 -tym rzucie. Wtedy
-tym rzucie. Wtedy
A) 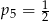 B)
B) 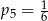 C)
C) 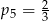 D)
D) 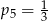
Samochód osobowy na dystansie 324 km spalił 20 litrów benzyny. Zakładając, że średnie zużycie paliwa nie ulegnie zmianie, ile benzyny spali ten samochód na dystansie 486 km?
A) 30 litrów. B) 28 litrów. C) 27 litrów. D) 32 litry.
Zadania otwarte
Zbiorem rozwiązań nierówności 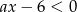 z niewiadomą
z niewiadomą  jest przedział
jest przedział 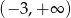 . Wyznacz
. Wyznacz  .
.
Wyznacz wszystkie liczby rzeczywiste, które są o 2 większe od swojej odwrotności.
Prostokąt jest wpisany w okrąg o promieniu 10, a jego dłuższe boki są styczne do okręgu o promieniu 3.
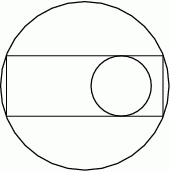
Oblicz pole tego prostokąta.
Uzasadnij, że jeżeli liczba całkowita  nie dzieli się przez 5, to
nie dzieli się przez 5, to 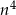 daje przy dzieleniu przez 5 resztę 1.
daje przy dzieleniu przez 5 resztę 1.
Ewa na początku 2015 roku kupiła skarbonkę i włożyła do niej 1000 zł. Na początku każdego kolejnego roku Ewa dokłada do skarbonki kwotę równą 20% dotychczas zgromadzonych oszczędności, a przez resztę roku nie dokłada, ani nie wybiera ze skarbonki żadnych pieniędzy. Ile będą wynosić oszczędności Ewy pod koniec roku 2020?
Proste 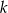 i
i 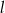 przecinają się w punkcie
przecinają się w punkcie 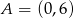 . Prosta
. Prosta 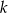 przecina ujemną półoś
przecina ujemną półoś 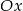 w punkcie
w punkcie 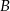 i tworzy z osiami układu trójkąt o polu 6, a prosta
i tworzy z osiami układu trójkąt o polu 6, a prosta 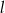 przecina dodatnią półoś
przecina dodatnią półoś 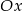 w punkcie
w punkcie 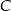 i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta
i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta 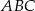 opuszczonej z wierzchołka
opuszczonej z wierzchołka 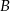 .
.
Rzucamy jednocześnie kostką i sześcioma symetrycznymi monetami. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, liczba otrzymanych oczek na kostce jest równa łącznej liczbie otrzymanych orłów na monetach.
Metalowy walec o objętości 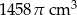 i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
Trzech znajomych: Jacek, Karol i Bogdan pokonało samochodami trasę pomiędzy miastami 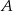 i
i 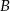 , przy czym Karol wyjechał pół godziny później niż Jacek i pół godziny wcześniej niż Bogdan. Cała trójka dojechała do miasta
, przy czym Karol wyjechał pół godziny później niż Jacek i pół godziny wcześniej niż Bogdan. Cała trójka dojechała do miasta 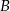 o tej samej godzinie. Średnia prędkość Jacka na całej trasie wyniosła 50 km/h, a Karola 60 km/h. Oblicz jaka była średnia prędkość Bogdana na tej trasie.
o tej samej godzinie. Średnia prędkość Jacka na całej trasie wyniosła 50 km/h, a Karola 60 km/h. Oblicz jaka była średnia prędkość Bogdana na tej trasie.

