Zadanie nr 6543569
Liczba  jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie 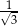 . Liczba
. Liczba 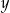 jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie 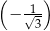 . Wynika stąd, że liczba
. Wynika stąd, że liczba 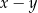 jest równa
jest równa
A) 0 B) 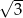 C)
C) 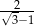 D) 3
D) 3
Rozwiązanie
Sposób I
Obliczamy sumy każdego z dwóch opisanych ciągów
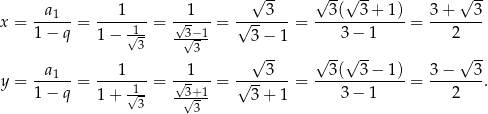
Stąd
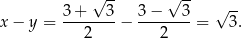
Sposób II
Mamy obliczyć różnicę
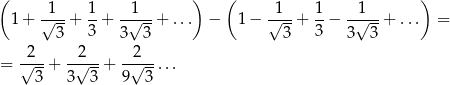
która jak widać jest sumą szeregu geometrycznego z pierwszym wyrazem równym 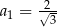 i ilorazem
i ilorazem 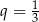 . Mamy zatem
. Mamy zatem
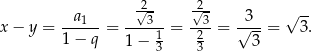
Z formalnego punktu widzenia, w powyższym rachunku skorzystaliśmy z tego, że zbieżny szereg geometryczny jest bezwględnie zbieżny – dzięki temu mogliśmy zmienić kolejność sumowania w wyrażeniu 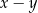 .
.
Odpowiedź: B

