Zadanie nr 9419567
Nieskończony malejący ciąg geometryczny 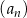 , określony dla
, określony dla 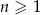 , spełnia warunki:
, spełnia warunki:
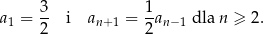
Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 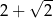 C)
C) 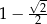 D)
D) 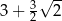
Rozwiązanie
Jeżeli 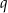 jest ilorazem ciągu
jest ilorazem ciągu 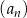 , to wiemy, że
, to wiemy, że
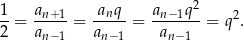
Wiemy ponadto, że ciąg jest monotoniczny, więc
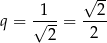
i suma wszystkich wyrazów tego ciągu jest równa
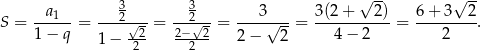
Odpowiedź: D

