Zadanie nr 2834829
Jeżeli środek okręgu wpisanego w trójkąt leży na wysokości trójkąta, to trójkąt ten musi być
A) rozwartokątny B) prostokątny C) równoramienny D) równoboczny
Rozwiązanie
Środek okręgu wpisanego to punkt przecięcia się dwusiecznych kątów wewnętrznych trójkąta.
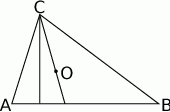
Skoro leży on na wysokości, powiedzmy opuszczonej na prostą 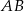 , to dwusieczna kąta
, to dwusieczna kąta 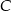 i wysokość muszą się pokrywać (bo obie przechodzą przez
i wysokość muszą się pokrywać (bo obie przechodzą przez 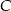 i
i 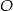 ). Trójkąt, w którym wysokość jest jednocześnie dwusieczną kąta jest trójkątem równoramiennym.
). Trójkąt, w którym wysokość jest jednocześnie dwusieczną kąta jest trójkątem równoramiennym.
Odpowiedź: C

