Ciąg arytmetyczny składa się z szesnastu wyrazów. Suma wyrazów o numerach parzystych jest równa 256, a suma wyrazów o numerach nieparzystych jest równa 240. Oblicz pierwszy i ostatni wyraz tego ciągu.
/Szkoła średnia/Ciągi
W ciągu arytmetycznym 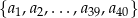 suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
O pewnym ciągu arytmetycznym wiadomo, że ma dziesięć wyrazów. Suma jego wyrazów o numerach nieparzystych jest równa 75, a suma wyrazów o numerach parzystych jest równa 90. Wyznacz pierwszy wyraz tego ciągu.
W ciągu arytmetycznym 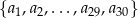 suma wyrazów tego ciągu o numerach parzystych jest równa 555, a suma wyrazów ciągu o numerach nieparzystych jest równa 615. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
suma wyrazów tego ciągu o numerach parzystych jest równa 555, a suma wyrazów ciągu o numerach nieparzystych jest równa 615. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
Ciąg 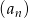 , gdzie
, gdzie 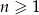 , jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji
, jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji 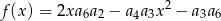 .
.
Dane są liczby dodatnie  i
i 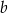 , dla których ciąg
, dla których ciąg 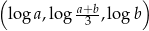 jest rosnącym ciągiem arytmetycznym. Oblicz różnicę tego ciągu.
jest rosnącym ciągiem arytmetycznym. Oblicz różnicę tego ciągu.
Cztery liczby tworzą ciąg geometryczny. Wyznacz te liczby wiedząc, że suma pierwszej i czwartej wynosi 36, a suma drugiej i trzeciej liczby wynosi 24.
Dany jest ciąg o wyrazie ogólnym 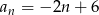 . Wybierz sto kolejnych początkowych wyrazów ciągu
. Wybierz sto kolejnych początkowych wyrazów ciągu 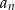 i oblicz dla jakiej liczby naturalnej
i oblicz dla jakiej liczby naturalnej 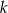 stosunek wyrazu stojącego na miejscu
stosunek wyrazu stojącego na miejscu 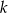 , licząc od początku, do wyrazu stojącego na miejscu
, licząc od początku, do wyrazu stojącego na miejscu 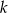 , licząc od końca, jest równy
, licząc od końca, jest równy 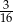 .
.
Obliczyć granicę 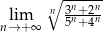 .
.
Liczby 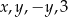 są kolejnymi wyrazami pewnego ciągu arytmetycznego. Znajdź liczbę
są kolejnymi wyrazami pewnego ciągu arytmetycznego. Znajdź liczbę  .
.
Ciąg 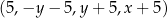 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Ciąg 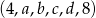 jest geometryczny. Oblicz
jest geometryczny. Oblicz 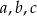 i
i 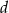 .
.
Liczby 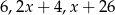 w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę
w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę  tego ciągu.
tego ciągu.
Liczby 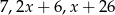 w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę
w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę  tego ciągu.
tego ciągu.
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 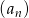 wyraża się wzorem
wyraża się wzorem 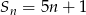 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz ciągu
-ty wyraz ciągu 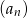 dla
dla 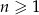 .
.
Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 26, różnica wyrazów czwartego i pierwszego wynosi 52. Oblicz piąty wyraz tego ciągu.
Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 21, różnica wyrazów czwartego i pierwszego wynosi 63. Oblicz piąty wyraz tego ciągu.
Długości boków 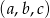 trójkąta tworzą ciąg geometryczny, przy czym kąt trójkąta leżący naprzeciwko boku długości
trójkąta tworzą ciąg geometryczny, przy czym kąt trójkąta leżący naprzeciwko boku długości 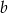 ma miarę
ma miarę 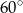 . Oblicz miary pozostałych kątów tego trójkąta.
. Oblicz miary pozostałych kątów tego trójkąta.
Długości wysokości trójkąta o bokach 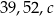 , gdzie
, gdzie 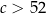 tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
Suma dziewięciu początkowych wyrazów ciągu arytmetycznego wynosi 18, a suma siedmiu początkowych wyrazów jest równa 0. Wyrazy: siódmy, ósmy i dziewiąty są długościami boków trójkąta. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu na nim opisanego.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego wynosi 6, a suma 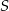 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 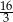 . Dla jakich naturalnych
. Dla jakich naturalnych  spełniona jest nierówność
spełniona jest nierówność 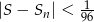 ?
?
Rozwiąż układ równań:
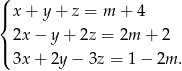
Dla jakich wartości parametru 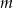 liczby
liczby 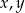 i
i  są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Długości boków trójkąta prostokątnego, którego obwód jest równy 24cm tworzą ciąg arytmetyczny. Oblicz
- długość wysokości poprowadzonej z wierzchołka kąta prostego;
- wartość wyrażenia
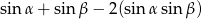 , gdzie
, gdzie  i
i 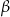 – miary kątów ostrych trójkąta.
– miary kątów ostrych trójkąta.
Dany jest ciąg arytmetyczny 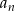 w którym
w którym 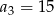 oraz
oraz 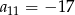 .
.
- Dla jakich
 zachodzi równość
zachodzi równość 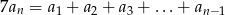 ?
? - Oblicz sumę pięćdziesięciu początkowych, ujemnych wyrazów ciągu
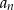 , które są podzielne przez 3.
, które są podzielne przez 3.
Wszystkie liczby parzyste z przedziału 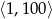 , które nie są podzielne przez 4 ustawiamy w ciąg
, które nie są podzielne przez 4 ustawiamy w ciąg 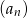 .
.
- Wyznacz wzór ciągu
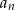 i uzasadnij, że jest on arytmetyczny.
i uzasadnij, że jest on arytmetyczny. - Oblicz sumę wszystkich wyrazów tego ciągu.
Liczby 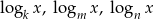 są kolejnymi wyrazami ciągu arytmetycznego, gdzie
są kolejnymi wyrazami ciągu arytmetycznego, gdzie 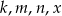 są różnymi od jedności liczbami dodatnimi. Uzasadnij, że
są różnymi od jedności liczbami dodatnimi. Uzasadnij, że 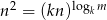 .
.

