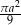Zadanie nr 1361982
W trójkąt równoboczny o boku długości  wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
Rozwiązanie
Dwie rzeczy, które będą nam niezbędne do rozwiązania tego zadania to wzór na promień okręgu wpisanego w trójkąt równoboczny o boku  i wzór na bok trójkąta równobocznego wpisanego w koło o promieniu
i wzór na bok trójkąta równobocznego wpisanego w koło o promieniu 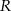 . Oba te wzory łatwo wynikają ze wzoru na wysokość w trójkącie równobocznym o boku
. Oba te wzory łatwo wynikają ze wzoru na wysokość w trójkącie równobocznym o boku 
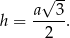
Promień  okręgu wpisanego w trójkąt równoboczny to
okręgu wpisanego w trójkąt równoboczny to 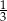 wysokości, czyli
wysokości, czyli
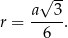
Natomiast promień okręgu 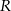 opisanego na tym trójkącie to
opisanego na tym trójkącie to  wysokości, czyli
wysokości, czyli
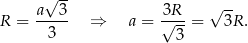
Spróbujmy teraz ustalić jak wyglądają promienie kół, o których mowa w treści zadania.
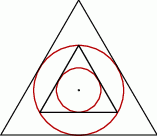
Pierwsze koło ma promień 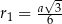 . Bok trójkąta równobocznego wpisanego w to koło ma długość
. Bok trójkąta równobocznego wpisanego w to koło ma długość
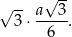
Zatem kolejne koło ma promień
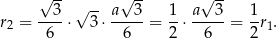
I tak dalej, kolejne koło będzie miało promień 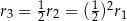 . Widać więc, że mamy do czynienia z kolejnymi wyrazami ciągu geometrycznego. Tak naprawdę, to mogliśmy sobie oszczędzić trochę rachunków i od razu zauważyć, że pierwsze i drugie koło to odpowiednio koła opisane i wpisane w drugi z trójkątów. Wystarczy teraz skorzystać z tego, że w trójkącie równobocznym promień okręgu opisanego jest dwa razy większy od promienia okręgu wpisanego.
. Widać więc, że mamy do czynienia z kolejnymi wyrazami ciągu geometrycznego. Tak naprawdę, to mogliśmy sobie oszczędzić trochę rachunków i od razu zauważyć, że pierwsze i drugie koło to odpowiednio koła opisane i wpisane w drugi z trójkątów. Wystarczy teraz skorzystać z tego, że w trójkącie równobocznym promień okręgu opisanego jest dwa razy większy od promienia okręgu wpisanego.
Musimy obliczyć sumę pól, czyli
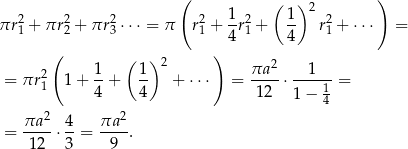
Odpowiedź: