Zadanie nr 1549090

Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 21 oraz suma ich odwrotności jest równa 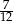172 .

Rozwiązanie

Sposób I

Oznaczmy szukane wyrazy przez 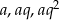a,aq,aq2 . Z podanej sumy mamy

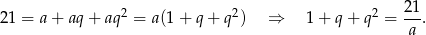
2 2 2 21- 21 = a + aq + aq = a(1+ q+ q ) ⇒ 1+ q+ q = a .

Napiszmy teraz warunek z sumą odwrotności.

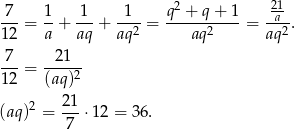
7 1 1 1 q2 + q + 1 2a1 12-= a-+ aq-+ aq2-= ---aq2----= aq2-. -7-= -2-1-- 12 (aq)2 21 (aq)2 = ---⋅1 2 = 36. 7

Ponieważ wyrazy ciągu są dodatnie, otrzymujemy stąd 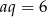aq = 6 . Uwzględniając to w pierwszym równaniu mamy

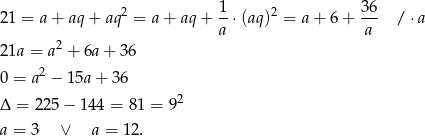
1 36 21 = a + aq + aq2 = a+ aq+ --⋅(aq)2 = a + 6 + --- / ⋅a a a 21a = a 2 + 6a + 36 2 0 = a − 15a + 36 Δ = 225 − 144 = 8 1 = 92 a = 3 ∨ a = 12.

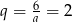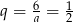Daje to odpowiednio 6 q = a = 2 i 6 1 q = a = 2 . Są zatem dwa takie ciągi

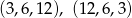
(3,6,12), (12,6,3)

Sposób II

Rachunki można odrobinę skrócić, jeżeli oznaczymy szukane liczby przez 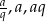a q,a,aq . Otrzymujemy wtedy równania

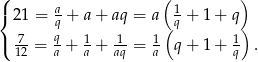
( ( ) { 21 = aq + a+ aq = a 1q + 1 + q 7 q 1 1 1 ( 1) ( 12 = a + a + aq = a q + 1 + q .

Dzieląc pierwsze równanie przez drugie mamy

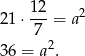
12- 2 21 ⋅ 7 = a 2 36 = a .

Stąd 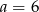a = 6 i pierwsze równanie przyjmuje postać

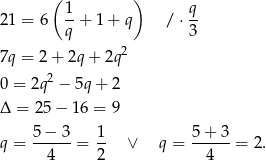
( 1 ) q 21 = 6 --+ 1+ q / ⋅ -- q 3 7q = 2 + 2q + 2q2 2 0 = 2q − 5q + 2 Δ = 25− 16 = 9 q = 5-−-3-= 1- ∨ q = 5-+-3-= 2 . 4 2 4

Tak jak poprzednio daje to nam dwa ciągi

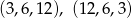
(3,6,12), (12,6,3)

Odpowiedź: (3,6,12 ),(1 2,6,3)