/Szkoła średnia/Ciągi

Zadanie nr 4645649

Dodaj do ulubionych
Dodaj do rozwiązanych

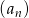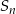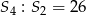Niech (an) oznacza ciąg geometryczny o wyrazach dodatnich, natomiast Sn niech oznacza sumę n początkowych wyrazów tego ciągu. Wiedząc, że S 4 : S 2 = 26 , oblicz q .

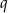Rozwiązanie

Sposób I

Rozpisujemy iloraz

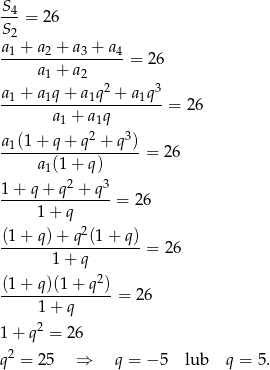
S4 ---= 2 6 S2 a1 +-a2 +-a-3 +-a4-= 26 a1 + a 2 a + a q+ a q2 + a q3 -1----1-----1------1--= 26 a1 + a1q a1(1+ q+ q2 + q 3) -------------------= 26 a1(1+ q) 1+ q+ q2 + q 3 ---------------= 26 1+ q (1+--q)+--q2(1+--q) 1+ q = 26 2 (1+--q)(1+--q-) 1+ q = 26 2 1+ q = 26 q2 = 25 ⇒ q = − 5 lub q = 5.

Ciąg ma mieć wyrazy dodatnie, więc 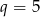q = 5 .

Sposób II

Jeżeli 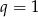q = 1 , to mamy równość

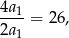
4a-1 2a 1 = 26,

która nie jest możliwa. Zatem 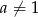a ⁄= 1 i możemy skorzystać ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego,

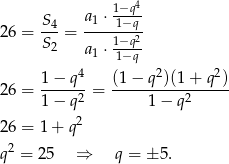
1−q4 S4- a1 ⋅-1−q- 26 = S2 = 1−q2 a1 ⋅ 1−q 1− q4 (1− q 2)(1 + q 2) 26 = -----2-= ----------2----- 1− q 1− q 26 = 1+ q2 2 q = 2 5 ⇒ q = ± 5.

Ciąg ma mieć wyrazy dodatnie, więc 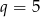q = 5 .  
Odpowiedź: q = 5

Wersja PDF