/Szkoła średnia/Ciągi

Zadanie nr 8990997

Dodaj do ulubionych
Dodaj do rozwiązanych

Siódmy wyraz ciągu geometrycznego 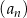(an) , określonego dla 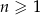n ≥ 1 , jest równy 6, a suma jego sześciu początkowych wyrazów jest równa 756. Iloraz 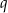q tego ciągu spełnia warunek: 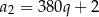a2 = 3 80q+ 2 . Oblicz pierwszy wyraz oraz iloraz tego ciągu.

Rozwiązanie

Wiemy, że

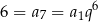
6 6 = a 7 = a1q

oraz

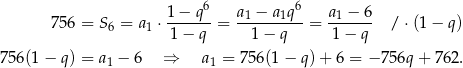
6 6 756 = S6 = a ⋅ 1-−-q-= a1 −-a1q-= a1-−-6 / ⋅(1− q) 1 1 − q 1− q 1− q 756(1 − q ) = a − 6 ⇒ a = 756(1 − q )+ 6 = − 756q + 762. 1 1

Wiemy ponadto, że

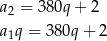
a2 = 380q + 2 a q = 380q + 2 1

Podstawiamy teraz w tej równości 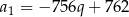a1 = −7 56q+ 762 .

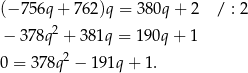
(− 756q + 762 )q = 380q + 2 / : 2 − 378q2 + 381q = 190q + 1 2 0 = 378q − 1 91q+ 1.

Rozwiązujemy teraz otrzymane równanie kwadratowe.

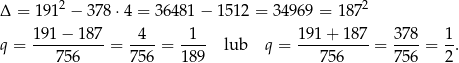
2 2 Δ = 191 − 37 8⋅4 = 36481 − 151 2 = 34969 = 187 191 − 187 4 1 19 1+ 187 378 1 q = ---756----= 756-= 18-9 lub q = ---7-56--- = 756-= 2.

Mamy wtedy odpowiednio

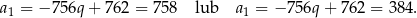
a1 = − 7 56q+ 762 = 75 8 lub a1 = − 756q + 762 = 384.

Zauważmy jeszcze, że w pierwszym przypadku

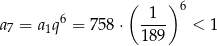
( ) 6 6 --1- a7 = a1q = 7 58⋅ 1 89 < 1

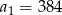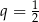W takim razie pozostaje druga możliwość: a1 = 38 4 i q = 1 2 . Łatwo sprawdzić, że przy tych danych spełnione są wszystkie warunki podane w treści zadania.  
Odpowiedź: 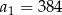a1 = 38 4 , q = 12

Wersja PDF