/Szkoła średnia/Ciągi

Zadanie nr 9015029

Dodaj do ulubionych
Dodaj do rozwiązanych

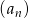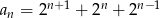Ciąg (an) określony jest wzorem n+ 1 n n−1 an = 2 + 2 + 2 .

  • Oblicz pierwszy i trzeci wyraz tego ciągu.
  • Uzasadnij, korzystając z definicji ciągu geometrycznego, że ciąg 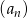(a ) n jest geometryczny.

Rozwiązanie

  • Liczymy
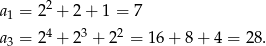
    a1 = 22 + 2 + 1 = 7 4 3 2 a3 = 2 + 2 + 2 = 16+ 8+ 4 = 28.

     
    Odpowiedź: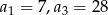 a1 = 7,a3 = 28

  • Musimy sprawdzić, czy iloraz dwóch kolejnych wyrazów jest stały (nie zależy od n ). Liczymy
    an+1 2n+2 + 2n+ 1 + 2n -----= -n+1----n----n−-1 = an 2 + 2 + 2 2(2n+1-+-2n-+-2n−-1) = 2n+ 1 + 2n + 2n−1 = 2.
Wersja PDF