/Szkoła średnia/Ciągi

Zadanie nr 9031903

Dodaj do ulubionych
Dodaj do rozwiązanych

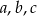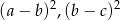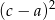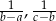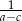Wykaż, że jeżeli żadne dwie spośród liczb a,b,c nie są równe oraz liczby (a − b)2,(b − c)2 i (c− a)2 tworzą ciąg arytmetyczny, to liczby b1−a,c−1b- i --1- a−c również tworzą ciąg arytmetyczny.

Rozwiązanie

Jeżeli trzy liczby 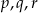p,q,r tworzą ciąg arytmetyczny to 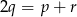2q = p + r , czyli

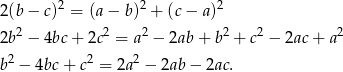
2 2 2 2 (b− c) = (a− b ) + (c − a) 2b 2 − 4bc + 2c2 = a2 − 2ab+ b2 + c2 − 2ac + a 2 2 2 2 b − 4bc + c = 2a − 2ab − 2ac.

A teraz popatrzmy na to, co mamy udowodnić.

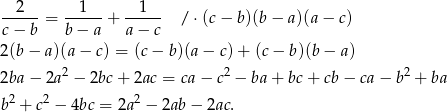
--2--= --1---+ --1-- / ⋅(c− b)(b− a)(a− c) c− b b − a a − c 2 (b− a )(a− c) = (c− b)(a − c) + (c − b)(b − a) 2 2 2 2ba − 2a − 2bc+ 2ac = ca − c − ba+ bc+ cb− ca − b + ba b 2 + c2 − 4bc = 2a 2 − 2ab − 2ac.

Jak już zauważyliśmy, prawdziwość tej równości wynika z założenia, co kończy dowód.

Wersja PDF