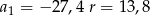/Szkoła średnia/Ciągi

Zadanie nr 9106101

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.

Rozwiązanie

Zapisujemy układ równań wynikający z założeń

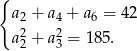
{ a2 + a4 + a6 = 42 a22 + a23 = 18 5.

Najpierw przekształcamy pierwsze równanie

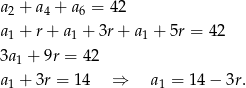
a2 + a4 + a6 = 42 a1 + r+ a1 + 3r+ a1 + 5r = 42 3a1 + 9r = 4 2 a1 + 3r = 14 ⇒ a1 = 14 − 3r.

Podstawiamy do drugiego równania

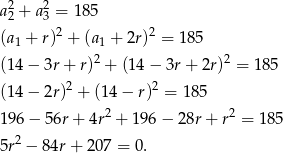
2 2 a2 + a3 = 185 (a1 + r)2 + (a1 + 2r)2 = 185 2 2 (14− 3r+ r) + (14 − 3r + 2r) = 18 5 (14− 2r)2 + (1 4− r)2 = 185 196− 56r+ 4r2 + 196 − 28r + r2 = 185 2 5r − 8 4r+ 2 07 = 0.

Liczymy wyróżnik i pierwiastki

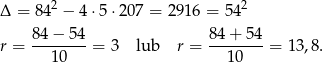
2 2 Δ = 84 − 4⋅5 ⋅207 = 2916 = 54 84-−-54- 84-+-5-4 r = 10 = 3 lub r = 10 = 13,8 .

Zatem

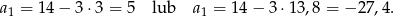
a1 = 14 − 3 ⋅3 = 5 lub a 1 = 14− 3⋅1 3,8 = − 27,4.

 
Odpowiedź: 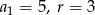a = 5, r = 3 1 lub a1 = − 2 7,4 r = 1 3,8

Wersja PDF