Zadanie nr 9337751
Dany jest ciąg 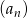 mający tę własność, że dla każdej liczby naturalnej
mający tę własność, że dla każdej liczby naturalnej  suma
suma  początkowych wyrazów tego ciągu jest równa
początkowych wyrazów tego ciągu jest równa 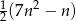 . Oblicz dwudziesty wyraz tego ciągu. Wykaż, że
. Oblicz dwudziesty wyraz tego ciągu. Wykaż, że 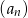 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Rozwiązanie
Oznaczmy sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 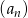 przez
przez 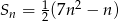 . W takim razie
. W takim razie
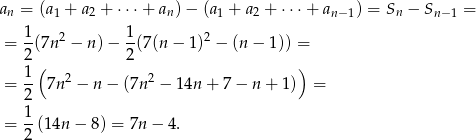
Powyższy rachunek ma sens o ile 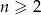 . Dla
. Dla 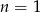 mamy
mamy 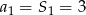 – zauważmy, że zgadza się to ze wzorem
– zauważmy, że zgadza się to ze wzorem 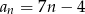 , więc możemy go używać również dla
, więc możemy go używać również dla 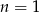 .
.
W szczególności mamy
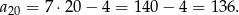
Aby wykazać, że ciąg 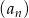 jest arytmetyczny musimy uzasadnić, że różnica jego kolejnych dwóch wyrazów jest stała, tzn. nie zależy od
jest arytmetyczny musimy uzasadnić, że różnica jego kolejnych dwóch wyrazów jest stała, tzn. nie zależy od  . Liczymy
. Liczymy
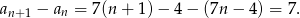
Widać, że zgodnie z oczekiwaniem, różnica jest stała.
Odpowiedź: