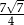/Szkoła średnia/Ciągi

Zadanie nr 9785666

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 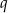q , a cosinus jednego z jego kątów jest równy q − 4 .

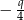  • Wyznacz q .
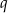  • Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość 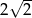√ -- 2 2 , oblicz pole tego trójkąta.

Rozwiązanie

Naszkicujmy trójkąt.

PIC

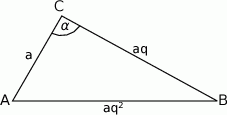
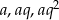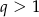Długości boków są kolejnymi wyrazami ciągu geometrycznego, więc są postaci a,aq,aq2 dla pewnego a . Wiemy ponadto, że ciąg ten jest rosnący, czyli q > 1 . To oznacza, że podany 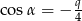cos α = − q 4 jest ujemny, czyli kąt α jest rozwarty. W takim razie musi on leżeć naprzeciwko najdłuższego boku trójkąta, czyli boku długości 2 aq .

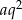  • Piszemy twierdzenie cosinusów.
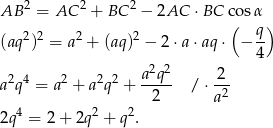
    2 2 2 AB = AC + BC − 2AC ⋅BC c(osα ) (aq2)2 = a2 + (aq)2 − 2⋅ a⋅aq ⋅ − q- 4 a2q2 2 a2q4 = a2 + a2q2 + ----- / ⋅-2- 2 a 2q4 = 2 + 2q2 + q2.

    Podstawiamy teraz 2 t = q .

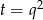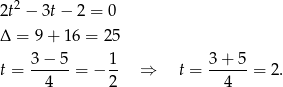
    2 2t − 3t− 2 = 0 Δ = 9 + 16 = 25 t = 3-−-5-= − 1- ⇒ t = 3+--5-= 2. 4 2 4

    Ujemne rozwiązanie odrzucamy i mamy 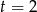t = 2 , czyli √ -- q = 2 .  
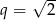    Odpowiedź: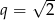 q = √ 2-

  • Aby wykorzystać informację o długości promienia okręgu opisanego, napiszemy twierdzenie sinusów. Zanim jednak to zrobimy obliczmy sinα .
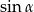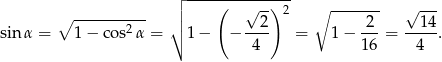
    ┌ --------------- ∘ ---------- ││ ( √ -) 2 ∘ ------- √ --- sin α = 1 − co s2α = ∘ 1− − --2- = 1− 2--= --14. 4 16 4

    Zatem na mocy twierdzenia sinusów mamy

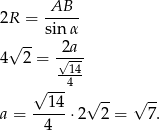
    AB--- 2R = sin α √ -- 2a 4 2 = -√-- -144- √ --- √ -- √ -- a = --14-⋅2 2 = 7. 4

    Teraz możemy obliczyć pole trójkąta korzystając ze wzoru z sinusem.

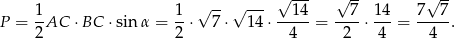
    -- --- √ --- √ -- √ -- P = 1-AC ⋅BC ⋅sin α = 1-⋅√ 7 ⋅√ 14 ⋅--1-4 = --7-⋅ 14-= 7--7. 2 2 4 2 4 4

     
    Odpowiedź: - 7√7- 4

Wersja PDF