/Szkoła średnia/Ciągi

Zadanie nr 9981876

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzy książki, których ceny tworzą ciąg geometryczny zakupiono płacąc łącznie 76 zł. Najdroższa z nich kosztowała o 4 zł mniej niż dwie pozostałe razem. Ile kosztowała każda książka?

Rozwiązanie

Oznaczmy ceny tych książek przez 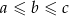a ≤ b ≤ c . To, że ceny książek tworzą ciąg geometryczny oznacza, że 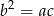b2 = ac . Otrzymujemy zatem układ równań

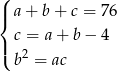
( |{ a+ b+ c = 76 |( c = a + b− 4 b2 = ac

Podstawiamy c z drugiego równania do pozostałych równań i otrzymujemy:

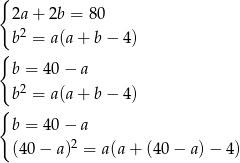
{ 2a + 2b = 8 0 2 b = a(a + b − 4) { b = 40 − a b2 = a(a + b − 4) { b = 40 − a (40 − a)2 = a(a + (40 − a) − 4)

Czyli

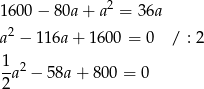
1600 − 8 0a+ a2 = 36a a2 − 116a + 16 00 = 0 / : 2 1 --a2 − 5 8a+ 800 = 0 2

Dalej liczymy standardowo

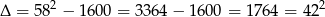
Δ = 5 82 − 1 600 = 336 4− 1600 = 17 64 = 422

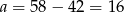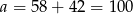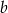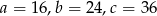Dostajemy stąd a = 58 − 42 = 16 lub a = 58 + 42 = 1 00 . Drugie z rozwiązań odrzucamy (bo daje ono ujemne b ) i otrzymujemy a = 16,b = 24,c = 36 .  
Odpowiedź: Ceny książek wynoszą 16,24 zł i 36 zł.

Wersja PDF