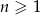/Szkoła średnia/Ciągi

Zadanie nr 9982446

Suma trzech początkowych wyrazów rosnącego ciągu geometrycznego 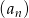(an) , określonego dla 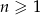n ≥ 1 , jest równa 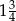134 . Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego 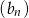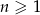(bn) , n ≥ 1 . Wyznacz wzór ciągu (bn) .

Wersja PDF

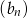Rozwiązanie

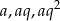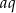Wiemy, że podane liczby tworzą ciąg geometryczny, więc możemy jest zapisać w postaci: a,aq,aq 2 . Wiemy ponadto, że a i aq są pierwszym i drugim wyrazem ciągu arytmetycznego 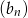(bn) , więc różnica tego ciągu jest równa 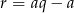r = aq − a . Dodatkowo, 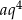aq4 jest czwartym wyrazem ciągu 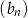(bn) , więc ze wzoru 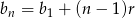bn = b1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy

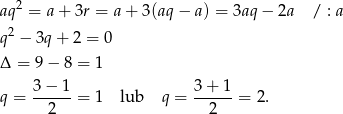
2 aq = a+ 3r = a + 3(aq − a) = 3aq − 2a / : a q 2 − 3q + 2 = 0 Δ = 9 − 8 = 1 3-−-1- 3-+-1- q = 2 = 1 lub q = 2 = 2.

Dany ciąg geometryczny ma być rosnący, więc mamy stąd 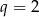q = 2 . Pozostało skorzystać z podanej sumy trzech pierwszych wyrazów ciągu (a ) n .

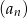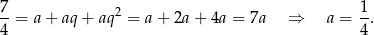
7- 2 1- 4 = a + aq + aq = a + 2a + 4a = 7a ⇒ a = 4.

To oznacza, że 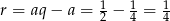r = aq − a = 1− 1= 1 2 4 4 i

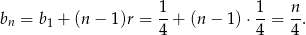
1- 1- n- bn = b1 + (n − 1)r = 4 + (n − 1) ⋅4 = 4.

 
Odpowiedź: 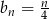bn = n 4 dla n ≥ 1

Wersja PDF