/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom rozszerzony grupa II 2 czerwca 2015 Czas pracy: 180 minut
Zadania zamknięte
Ile rozwiązań ma równanie 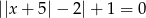 ?
?
A) 0 B) 2 C) 4 D) 6
Reszta z dzielenia wielomianu 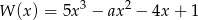 przez dwumian
przez dwumian 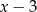 jest równa 88. Zatem
jest równa 88. Zatem
A) 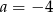 B)
B) 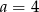 C)
C) 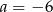 D)
D) 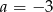
Jeżeli 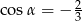 i
i 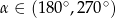 to
to
A) 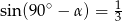
B) 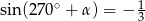
C) 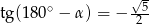
D) 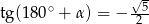
Okrąg 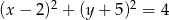 jest styczny do prostej
jest styczny do prostej
A) 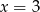 B)
B) 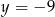 C)
C) 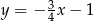 D)
D) 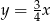
Jeżeli 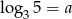 to wyrażenie
to wyrażenie 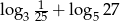 jest równe
jest równe
A)  B)
B) 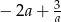 C)
C) 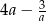 D)
D) 
Zadania otwarte
W trójkącie kąt między bokami o długościach 6 i 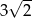 jest równy
jest równy 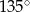 . Jaką długość ma trzeci bok trójkąta?
. Jaką długość ma trzeci bok trójkąta?
Określono ciąg wzorem rekurencyjnym: 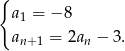 Jaką wartość ma 5 wyraz tego ciągu?
Jaką wartość ma 5 wyraz tego ciągu?
Przybliżenie z niedomiarem liczby  jest równe 12, a błąd względny tego przybliżenia wynosi 0,0125. Wyznacz liczbę
jest równe 12, a błąd względny tego przybliżenia wynosi 0,0125. Wyznacz liczbę  .
.
Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych nieparzystych jest podzielna przez 3.
Wykaż, że jeżeli każda przekątna czworokąta dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.
Dla jakich wartości parametru 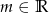 suma sześcianów dwóch różnych miejsc zerowych funkcji
suma sześcianów dwóch różnych miejsc zerowych funkcji 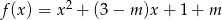 jest nieujemna?
jest nieujemna?
Dla jakich wartości parametru 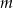 rozwiązaniem układu równań
rozwiązaniem układu równań 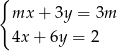 jest para liczb nieujemnych?
jest para liczb nieujemnych?
Z drutu o długości 320 cm zbudowano ramkę w kształcie prostokąta. Jakie powinna mieć wymiary aby pole prostokąta było największe?
Na rysunku przedstawiono wykres funkcji 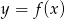 .
.
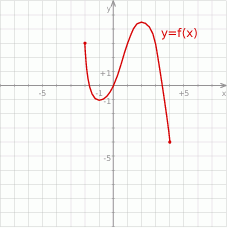
Naszkicuj wykres funkcji: 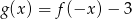 . Określ dziedzinę oraz miejsca zerowe funkcji
. Określ dziedzinę oraz miejsca zerowe funkcji 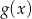 .
.
Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.
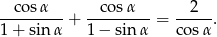
Wyznacz resztę z dzielenia wielomianu 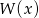 przez wielomian
przez wielomian 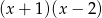 wiedząc, że
wiedząc, że 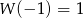 i
i 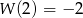 .
.
Na trapezie 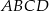 można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe
można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe 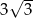 .
.
Trzy liczby tworzą ciąg arytmetyczny o 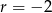 . Jeżeli pierwszą powiększymy o 3 drugą o 1 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
. Jeżeli pierwszą powiększymy o 3 drugą o 1 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.

