/Szkoła średnia/Zadania maturalne/Matura 2017
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 29 kwietnia 2017 Czas pracy: 170 minut
Zadania zamknięte
Wskaż nierówność, którą spełnia liczba 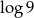 .
.
A) 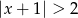 B)
B) 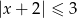 C)
C) 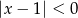 D)
D) 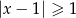
Liczba 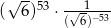 jest równa
jest równa
A) 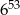 B)
B) 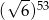 C) 1 D) 0
C) 1 D) 0
Pierwsza rata, która stanowi 9% ceny kanapy, jest o 84 zł niższa od drugiej raty, która stanowi 12% ceny kanapy. Kanapa kosztuje
A) 280 zł B) 2788 zł C) 2520 zł D) 2800 zł
Funkcja liniowa określona wzorem 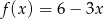 przyjmuje wartości ujemne dla:
przyjmuje wartości ujemne dla:
A) 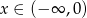 B)
B) 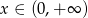 C)
C) 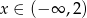 D)
D) 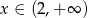
Na rysunku jest przedstawiony wykres funkcji 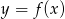 .
.
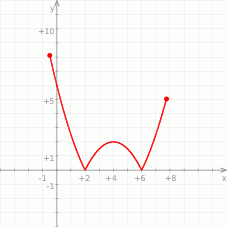
Które równanie ma dokładnie jedno rozwiązanie?
A) 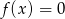 B)
B) 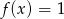 C)
C) 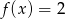 D)
D) 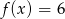
Układ równań 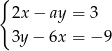 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 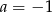 B)
B) 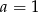 C)
C) 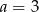 D)
D) 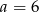
Kąt  jest kątem ostrym i
jest kątem ostrym i 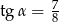 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 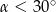 B)
B) 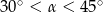 C)
C) 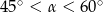 D)
D) 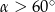
Nieskończony ciąg liczbowy 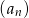 , w którym
, w którym
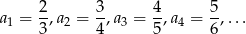
może być opisany wzorem:
A) 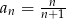 B)
B) 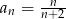 C)
C) 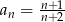 D)
D) 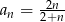
Liczba 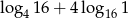 jest równa
jest równa
A) 16 B) 2 C) 4 D) 6
Najmniejszą wartość w przedziale 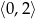 funkcja kwadratowa
funkcja kwadratowa 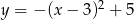 przyjmuje dla argumentu
przyjmuje dla argumentu
A) 2 B) 0 C) 3 D) 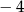
Funkcja liniowa określona jest wzorem 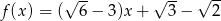 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 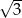 B)
B) 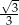 C)
C) 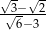 D)
D) 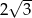
Dany jest nieskończony rosnący ciąg arytmetyczny 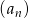 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 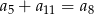 B)
B) 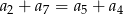 C)
C) 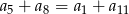 D)
D) 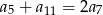
Wiadomo, że 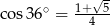 . Zatem
. Zatem
A) 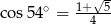 B)
B) 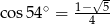 C)
C) 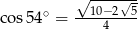 D)
D) 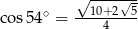
Punkt 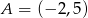 leży na prostej
leży na prostej 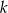 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 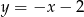 . Prosta
. Prosta 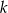 ma równanie
ma równanie
A) 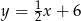 B)
B) 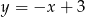 C)
C) 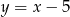 D)
D) 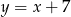
Przekątne rombu mają długości 12 i 10. Obwód tego rombu jest równy
A) 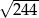 B)
B) 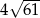 C)
C) 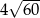 D)
D) 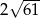
Na rysunku 1 jest przedstawiony wykres funkcji 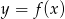 .
.
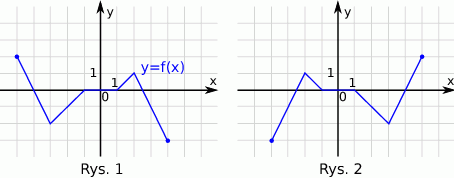
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 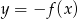 B)
B) 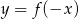 C)
C) 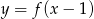 D)
D) 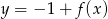
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 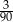 B)
B) 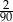 C)
C) 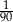 D)
D) 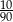
W ciągu geometrycznym 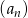 mamy
mamy 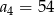 i
i 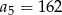 . Wtedy wyraz
. Wtedy wyraz 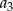 jest równy
jest równy
A) 6 B) 18 C) 2 D) 27
Punkty 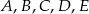 leżące na okręgu o środku
leżące na okręgu o środku 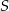 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 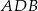 jest równa
jest równa
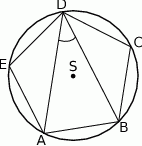
A) 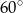 B)
B) 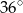 C)
C) 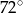 D)
D) 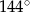
Grupa przypadkowych przechodniów została poproszona o odpowiedź na pytanie: „ile osób liczy Państwa rodzina?”. Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba odpowiedzi |
| 2 | 6 |
| x | 12 |
| 5 | 2 |
Średnia liczba osób w rodzinie dla pytanych osób jest równa 3,5. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 1 D) 7
Odcinki 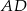 i
i 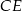 są wysokościami trójkąta
są wysokościami trójkąta 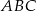 .
.
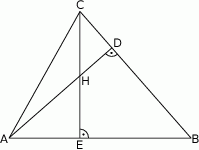
Zatem
A) 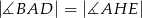
B) 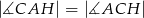
C) 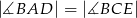
D) 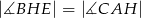
Latawiec ma wymiary podane na rysunku. Powierzchnia zacieniowanego trójkąta jest równa
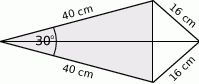
A) 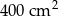 B)
B) 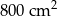 C)
C) 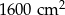 D)
D) 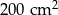
Które z poniższych zdań nie jest prawdziwe?
A) W każdy romb można wpisać okrąg.
B) W każdy prostokąt można wpisać okrąg.
C) Na każdym prostokącie można opisać okrąg.
D) W każdy deltoid można wpisać okrąg.
Liczba przekątnych sześcianu to
A) 6 B) 12 C) 8 D) 4
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 12 jest równa
A) 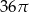 B)
B) 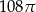 C)
C) 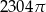 D)
D) 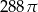
Zadania otwarte
Rozwiąż nierówność 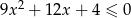 .
.
Dany ciąg arytmetyczny 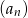 taki, że
taki, że 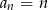 , dla
, dla 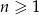 . Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez
. Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez 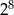 .
.
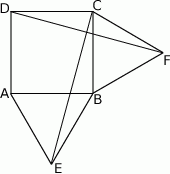
Na zewnątrz kwadratu 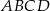 na bokach
na bokach 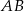 i
i 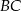 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 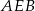 i
i 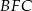 . Uzasadnij, że proste
. Uzasadnij, że proste 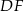 i
i 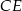 są prostopadłe.
są prostopadłe.
W równoległoboku, który nie jest prostokątem, krótsza przekątna dzieli go na dwa równoramienne trójkąty prostokątne. Krótszy bok równoległoboku ma długość 8. Oblicz pole tego równoległoboku.
Liczby 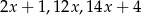 są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz  .
.
Ze zbioru liczb 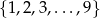 losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.
losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.
Okrąg o środku w punkcie 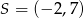 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 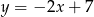 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Dwa samochody osobowe wyjechały z miast 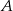 i
i 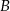 oddalonych od siebie o 480 km. Samochód jadący z miasta
oddalonych od siebie o 480 km. Samochód jadący z miasta 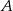 do miasta
do miasta 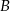 wyjechał o pół godziny wcześniej niż samochód jadący z miasta
wyjechał o pół godziny wcześniej niż samochód jadący z miasta 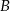 do miasta
do miasta 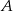 i jechał z prędkością o 16 km/h mniejszą. Samochody te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te samochody.
i jechał z prędkością o 16 km/h mniejszą. Samochody te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te samochody.
Podstawą ostrosłupa 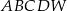 jest kwadrat
jest kwadrat 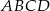 . Krawędź boczna
. Krawędź boczna 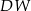 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 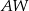 i
i 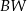 mają następujące długości:
mają następujące długości: 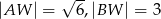 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.