/Szkoła średnia/Zadania maturalne/Matura 2017
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony
(stara formuła) 2 czerwca 2017 Czas pracy: 180 minut
Rozwiąż równanie 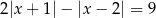 .
.
Wykaż, że dla 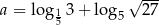 i
i 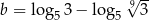 prawdziwa jest równość
prawdziwa jest równość 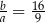 .
.
Ciąg 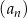 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 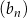 jest geometryczny. Pierwszy wyraz
jest geometryczny. Pierwszy wyraz 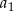 ciągu arytmetycznego jest ilorazem ciągu geometrycznego
ciągu arytmetycznego jest ilorazem ciągu geometrycznego 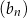 . Wyrazy ciągu
. Wyrazy ciągu 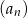 są liczbami całkowitymi, a suma ośmiu początkowych wyrazów tego ciągu jest równa 124. Natomiast pierwszy wyraz
są liczbami całkowitymi, a suma ośmiu początkowych wyrazów tego ciągu jest równa 124. Natomiast pierwszy wyraz 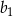 ciągu geometrycznego jest różnicą ciągu arytmetycznego
ciągu geometrycznego jest różnicą ciągu arytmetycznego 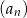 . Suma dwóch pierwszych wyrazów ciągu geometrycznego
. Suma dwóch pierwszych wyrazów ciągu geometrycznego 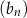 jest równa 18. Wyznacz te ciągi.
jest równa 18. Wyznacz te ciągi.
Rozwiąż równanie 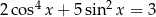 w przedziale
w przedziale 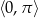 .
.
Miary kątów trójkąta 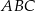 są równe
są równe 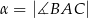 ,
, 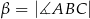 i
i 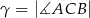 . Punkt
. Punkt 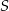 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 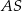 i
i 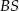 przecinają boki
przecinają boki 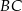 i
i 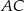 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 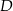 i
i  (zobacz rysunek).
(zobacz rysunek).
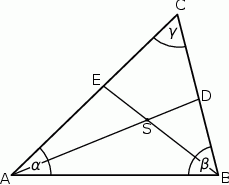
Wykaż, że jeżeli 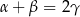 , to na czworokącie
, to na czworokącie 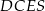 można opisać okrąg.
można opisać okrąg.
Prosta 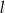 , na której leży punkt
, na której leży punkt 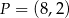 , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej
, tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej 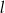 .
.
Podstawą ostrosłupa 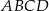 jest trójkąt równoramienny o podstawie
jest trójkąt równoramienny o podstawie 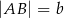 i kącie
i kącie  pomiędzy ramionami. Krawędź
pomiędzy ramionami. Krawędź 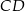 jest wysokością ostrosłupa, a kąt nachylenia ściany
jest wysokością ostrosłupa, a kąt nachylenia ściany 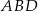 do podstawy ostrosłupa jest równy
do podstawy ostrosłupa jest równy 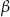 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Z cyfr 0, 1, 2 tworzymy pięciocyfrowe liczby całkowite dodatnie podzielne przez 15. Oblicz, ile możemy utworzyć takich liczb.
Wyznacz wszystkie wartości parametru 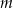 , dla których równanie
, dla których równanie 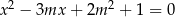 ma dwa różne rozwiązania takie, że każde należy do przedziału
ma dwa różne rozwiązania takie, że każde należy do przedziału 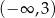 .
.
Trapez równoramienny 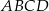 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 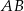 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 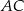 i
i 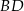 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 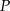 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 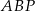 .
.
Prawdopodobieństwo tego, że z pewnej grupy osób wylosujemy osobę znającą język angielski jest równe 0,4, prawdopodobieństwo wylosowania osoby znającej język francuski jest równe 0,2, natomiast prawdopodobieństwo wylosowania osoby znającej oba te języki jest równe 0,1. Wykaż, że prawdopodobieństwo wylosowania osoby, która zna język angielski i nie zna języka francuskiego jest trzy razy większe od prawdopodobieństwa wylosowania osoby, która zna język francuski i nie zna języka angielskiego.

