/Szkoła średnia/Zadania maturalne/Matura 2017/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 8 kwietnia 2017 Czas pracy: 180 minut
Zadania zamknięte
Funkcja 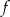 określona jest wzorem
określona jest wzorem 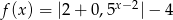 dla każdej liczby rzeczywistej. Zbiorem wartości funkcji
dla każdej liczby rzeczywistej. Zbiorem wartości funkcji 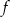 jest
jest
A) 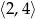 B)
B) 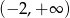 C)
C) 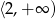 D)
D) 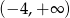
Wielomian 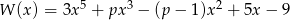 jest podzielny przez dwumian
jest podzielny przez dwumian 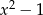 dla
dla 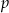 równego
równego
A) 6 B) 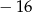 C) 4 D)
C) 4 D) 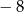
Ciąg 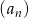 jest określony wzorem
jest określony wzorem 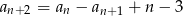 dla każdej liczby naturalnej
dla każdej liczby naturalnej 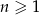 . Wiadomo ponadto, że
. Wiadomo ponadto, że 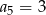 i
i 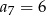 . Szósty wyraz tego ciągu jest równy
. Szósty wyraz tego ciągu jest równy
A) 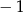 B)
B) 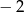 C) 3 D) 5
C) 3 D) 5
W ostrosłupie prawidłowym czworokątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Wynika stąd, że cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
A) 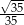 B)
B) 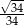 C)
C) 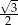 D)
D) 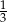
Granica 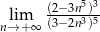 jest równa
jest równa
A) 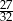 B)
B)  C)
C) 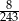 D)
D) 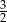
Zadania otwarte
Suma wszystkich wyrazów ciągu danego wzorem 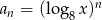 , gdzie
, gdzie 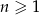 jest równa
jest równa 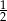 . Oblicz
. Oblicz  .
.
Dany jest trójkąt prostokątny o polu 6, w którym długość przeciwprostokątnej jest liczbą z przedziału 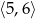 . Wykaż, że suma długości przyprostokątnych tego trójkąta jest liczbą z przedziału
. Wykaż, że suma długości przyprostokątnych tego trójkąta jest liczbą z przedziału 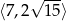 .
.
Funkcja 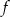 określona jest wzorem
określona jest wzorem 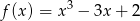 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 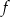 , które przechodzą przez punkt
, które przechodzą przez punkt 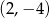 .
.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych 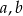 prawdziwa jest nierówność
prawdziwa jest nierówność
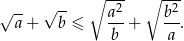
W pudełku znajdują się 4 kostki do gry: 3 sześcienne (ze ścianami ponumerowanymi liczbami od 1 do 6) i jedna czworościenna (ze ścianami ponumerowanymi liczbami od 1 do 4). Losowo wybrano kostkę, wykonano nią 3 rzuty i w wyniku tych 3 rzutów otrzymano trzy razy jedynkę. Jakie jest prawdopodobieństwo, że wybrana kostka była kostką czworościenną?
Rozwiąż równanie 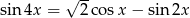 w przedziale
w przedziale 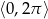 .
.
W czworokąt 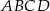 , w którym
, w którym 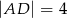 i
i 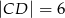 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 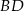 tworzy z bokiem
tworzy z bokiem 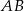 czworokąta kąt o mierze
czworokąta kąt o mierze 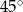 , natomiast z bokiem
, natomiast z bokiem 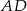 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy 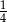 . Wyznacz długości boków
. Wyznacz długości boków 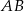 i
i 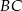 oraz długość przekątnej
oraz długość przekątnej 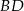 tego czworokąta.
tego czworokąta.
Wyznacz wszystkie wartości parametru  , dla których wykresy funkcji
, dla których wykresy funkcji 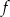 i
i 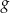 , określonych wzorami
, określonych wzorami 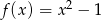 oraz
oraz 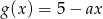 , przecinają w dwóch punktach znajdujących się powyżej osi
, przecinają w dwóch punktach znajdujących się powyżej osi 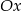 układu współrzędnych.
układu współrzędnych.
Punkty 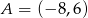 i
i 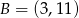 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego 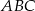 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 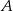 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 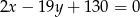 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 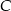 .
.
Podstawa stożka o kącie rozwarcia 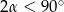 jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu
jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu  .
.
Na bokach 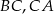 i
i 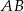 trójkąta
trójkąta 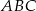 wybrano punkty
wybrano punkty 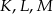 takie, że
takie, że

Wyznacz wartość 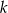 , dla której stosunek pola trójkąta
, dla której stosunek pola trójkąta 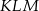 do pola trójkąta
do pola trójkąta 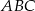 jest najmniejszy.
jest najmniejszy.

