Zadanie nr 4602131
Zbadaj, czy istnieje taka wartość współczynnika  , dla której wielomiany
, dla której wielomiany 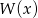 i
i ![[Q (x)]2](https://img.zadania.info/zad/4602131/HzadT2x.gif) są równe, jeśli
są równe, jeśli 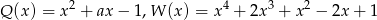 .
.
Rozwiązanie
Wykonujemy obliczenia
![2 2 2 [Q (x)] = (x + ax − 1) = = x 4 + ax 3 − x2 + ax3 + a2x2 − ax − x2 − ax + 1 = 4 3 2 2 = x + 2ax + x (a − 2)− 2ax + 1](https://img.zadania.info/zad/4602131/HzadR0x.gif)
Jeżeli wielomiany mają być równe to współczynniki przy odpowiadających sobie potęgach  muszą być równe. Zatem
muszą być równe. Zatem
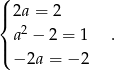
Z pierwszego równania mamy, że 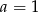 natomiast z drugiego, że
natomiast z drugiego, że 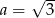 , czyli układ jest sprzeczny. Zatem nie istnieje współczynnik
, czyli układ jest sprzeczny. Zatem nie istnieje współczynnik  taki, że
taki, że 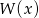 i
i ![2 [Q (x)]](https://img.zadania.info/zad/4602131/HzadR7x.gif) będą równe.
będą równe.
Odpowiedź: Nie, nie istnieje.

