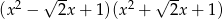/Szkoła średnia/Funkcje/Wielomiany/Stopnia 4

Zadanie nr 4821178

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozłóż na czynniki drugiego stopnia wielomian 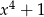4 x + 1 .

Rozwiązanie

Sposób I

Przekształcamy

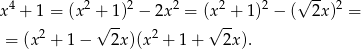
4 2 2 2 2 2 √ -- 2 x + 1 = (x +√ -1) − 2x = (x√ -+ 1) − ( 2x) = = (x 2 + 1 − 2x )(x2 + 1+ 2x).

Sposób II

Szukamy rozkładu postaci

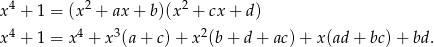
x 4 + 1 = (x2 + ax+ b)(x2 + cx + d) 4 4 3 2 x + 1 = x + x (a+ c)+ x (b+ d+ ac)+ x(ad+ bc)+ bd.

Mamy zatem układ równań

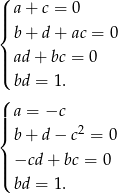
( ||| a+ c = 0 { b+ d+ ac = 0 | ad + bc = 0 ||( bd = 1. ( ||| a = −c { b+ d− c2 = 0 |||( −cd + bc = 0 bd = 1.

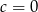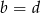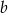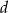Równość c = 0 łatwo prowadzi do sprzeczności, zatem z trzeciego równania mamy b = d . Z drugiego równania wynika, że b i d muszą być dodatnie, zatem z ostatniego 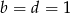b = d = 1 . Drugie równanie daje c = ± √ 2- .  
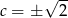Odpowiedź: 2 √ -- 2 √ -- (x − 2x + 1)(x + 2x+ 1)

Wersja PDF