/Szkoła średnia/Zadania maturalne/Matura 2019/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 4 maja 2019 Czas pracy: 170 minut
Zadania zamknięte
Wyrażenie 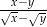 jest równe
jest równe
A) 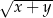 B)
B) 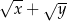 C)
C) 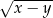 D)
D) 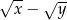
Liczba ![[ ] log3 log64(log√ 39)](https://img.zadania.info/zes/0079423/HzesT5x.gif) jest równa
jest równa
A) 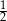 B)
B) 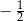 C) 1 D)
C) 1 D) 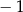
Liczbami spełniającymi równanie 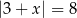 są
są
A) 11 i 5 B) 3 i 8 C) 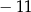 i 5 D)
i 5 D) 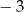 i 8
i 8
Badając pewien roztwór stwierdzono, że zawiera on 0,06 g chloru, co stanowi 0,04% masy roztworu. Jaka była masa roztworu?
A) 1,5 kg B) 15 g C) 150 g D) 1,5 g
Nierówność 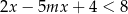 jest spełniona przez każdą liczbę rzeczywistą jeżeli
jest spełniona przez każdą liczbę rzeczywistą jeżeli
A) 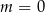 B)
B) 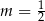 C)
C) 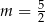 D)
D) 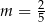
Rozwiązaniem równania 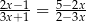 jest
jest
A) 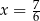 B)
B) 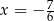 C)
C) 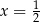 D)
D) 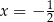
Kwotę 1000 zł wpłacamy do banku na 3 lata. Kapitalizacja odsetek jest dokonywana w tym banku co kwartał, a roczna stopa procentowa wynosi 8%. Po trzech latach otrzymamy kwotę
A) 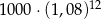 B)
B) 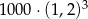 C)
C) 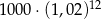 D)
D) 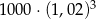
Liczba 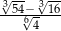 jest równa
jest równa
A) 2 B) 1 C) 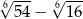 D)
D) 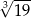
Na rysunku przedstawiony jest wykres funkcji 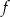 .
.
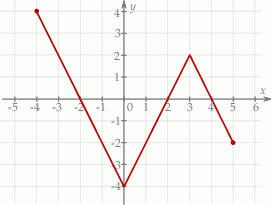
Maksymalnym zbiorem, w którym funkcja  przyjmuje tylko wartości ujemne, jest
przyjmuje tylko wartości ujemne, jest
A) 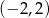 B)
B) 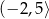 C)
C) 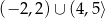 D)
D) 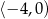
Zbiorem wartości funkcji 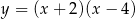 jest przedział
jest przedział
A) 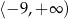 B)
B) 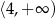 C)
C) 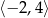 D)
D) 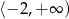
Poniżej zamieszczono fragment tabeli wartości funkcji liniowej
 | 1 | 2 | 4 |
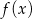 | 4 | 1 |
W pustym miejscu w tabeli powinna znajdować się liczba:
A) 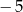 B) 5 C)
B) 5 C) 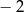 D) 2
D) 2
Wykres funkcji kwadratowej 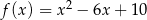 powstaje z wykresu funkcji
powstaje z wykresu funkcji 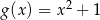 przez przesunięcie o 3 jednostki
przez przesunięcie o 3 jednostki
A) w prawo B) w lewo C) w górę D) w dół
Ciągiem geometrycznym jest ciąg określony wzorem
A) 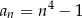 B)
B) 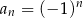 C)
C) 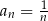 D)
D) 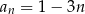
Ciąg 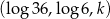 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 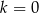 B)
B) 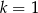 C)
C) 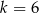 D)
D) 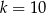
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 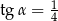 . Zatem
. Zatem
A) 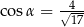 B)
B) 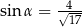 C)
C) 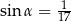 D)
D) 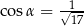
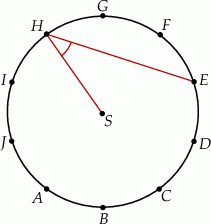
Punkty 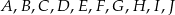 dzielą okrąg o środku
dzielą okrąg o środku 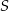 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 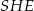 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 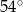 B)
B) 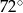 C)
C) 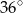 D)
D) 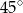
Dany jest trójkąt o wierzchołkach 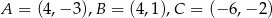 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 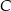 jest równa
jest równa
A) 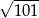 B)
B) 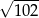 C)
C) 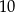 D)
D) 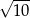
Krótsza przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła wpisanego w ten sześciokąt jest równe
A) 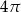 B)
B) 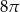 C)
C) 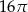 D)
D) 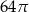
Stosunek długości trzech krawędzi prostopadłościanu o objętości 240 jest równy 2:3:5. Pole powierzchni tego prostopadłościanu jest równe:
A) 124 B) 248 C) 496 D) 62
Z prostokąta  o polu 30 wycięto trójkąt
o polu 30 wycięto trójkąt  (tak jak na rysunku). Pole zacieniowanej figury jest równe
(tak jak na rysunku). Pole zacieniowanej figury jest równe
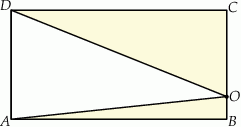
A) 7,5 B) 15 C) 20 D) 25
Objętość stożka o wysokości 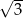 i kącie rozwarcia
i kącie rozwarcia 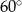 jest równa
jest równa
A) 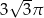 B)
B) 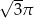 C)
C) 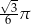 D)
D) 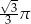
Mediana uporządkowanego niemalejąco zestawu liczb: 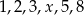 nie zmienia się po dopisaniu liczby 10. Wtedy
nie zmienia się po dopisaniu liczby 10. Wtedy
A) 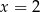 B)
B) 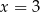 C)
C) 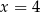 D)
D) 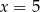
Liczba wszystkich krawędzi graniastosłupa jest o 12 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Każdy bok trójkąta prostokątnego o bokach 3, 4, 5 kolorujemy jednym z 6 kolorów tak, aby żadne dwa boki nie były pokolorowane tym samym kolorem. Ile jest takich pokolorowań?
A) 15 B) 120 C) 216 D) 20
Ze zbioru dzielników naturalnych liczby 8 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 4 jest równe
A) 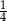 B)
B) 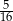 C)
C)  D)
D) 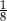
Zadania otwarte
Rozwiąż nierówność 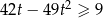 .
.
Wyznacz najmniejszą i największą wartość funkcji 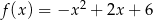 w przedziale
w przedziale 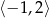 .
.
Udowodnij, że jeżeli liczby 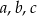 są kolejnymi wyrazami ciągu geometrycznego, to
są kolejnymi wyrazami ciągu geometrycznego, to
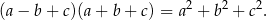
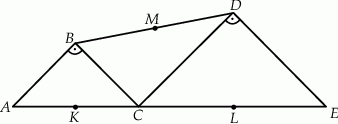
Trójkąty 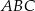 i
i 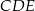 są równoramienne i prostokątne. Punkty
są równoramienne i prostokątne. Punkty 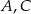 i
i 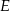 leżą na jednej prostej, a punkty
leżą na jednej prostej, a punkty 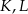 i
i 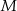 są środkami odcinków
są środkami odcinków 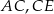 i
i 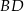 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 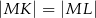 .
.
Kąt  jest ostry i
jest ostry i 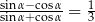 . Oblicz
. Oblicz 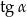 .
.
W 8 pudełkach umieszczamy 5 ponumerowanych kulek tak, aby w żadnym pudełku nie było więcej niż jednej kulki. Na ile sposobów możemy to zrobić?
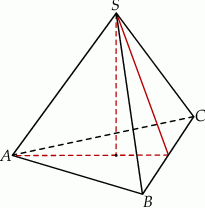
Objętość ostrosłupa prawidłowego trójkątnego 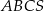 (tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę  tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
Liczby 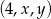 są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę
są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę  zwiększymy o 1, a liczbę
zwiększymy o 1, a liczbę 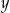 zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz
zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz  i
i 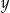 .
.
Punkty 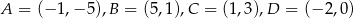 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 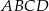 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.

