/Gimnazjum/Egzamin gimnazjalny/Egzamin 2019/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 23 marca 2019 Czas pracy: 90 minut
Informacja do zadań 1 i 2
W trakcie przygotowań do zawodów pływackich Szymon i Bartosz pływali równolegle do brzegu jeziora na dystansie 2 km. Wykresy przedstawiają zależność między odległością chłopców od miejsca startu, a czasem pływania.
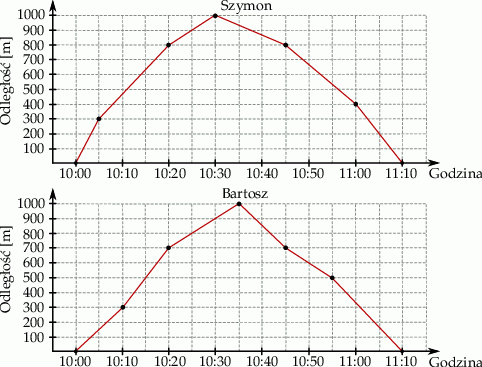
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bartosz pokonał dystans 2 km ze średnią prędkością większą niż Szymon. | P | F |
| Bartosz przepłynął obie połowy dystansu 2 km z tą samą prędkością średnią. | P | F |
Ile razy między godziną 10:05 a 11:05 Szymon i Bartosz znajdowali się w tej samej odległości od miejsca startu?
Wybierz odpowiedź spośród podanych.
A) 0 B) 1 C) 2 D) 4
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Różnica liczb MCC i DCXXXIX jest równa
A) DXXXIX B) DXLI C) DLXI D) MDCCCXXXIX
Która z liczb nie może być średnią arytmetyczną liczby uczniów w czterech klasach trzecich?
Wybierz odpowiedź spośród podanych.
A) 23,4 B) 25,5 C) 27,25 D) 21,75
Tomek wyciął z papieru 15 trójkątów oraz pewną liczbę czworokątów. Gdyby rozciął każdy z czworokątów na dwa trójkąty, to liczba trójkątów zwiększyłaby się o 80%.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba czworokątów, które Tomek wyciął z papieru jest równa
A) 4 B) 3 C) 6 D) 8
W ostatnim dniu każdego miesiąca ubiegłego roku pani Urszula zapisywała masę swojego ciała. Początkowo masa jej ciała rosła. W lipcu ważyła tylko samo, ile w listopadzie i mniej niż w marcu. W żadnym miesiącu nie ważyła mniej niż 52 kg. Pani Urszula wyniki swoich pomiarów umieściła na diagramie.
Który z diagramów przedstawia wyniki pomiarów pani Urszuli w ubiegłym roku? Wybierz właściwą odpowiedź spośród podanych.
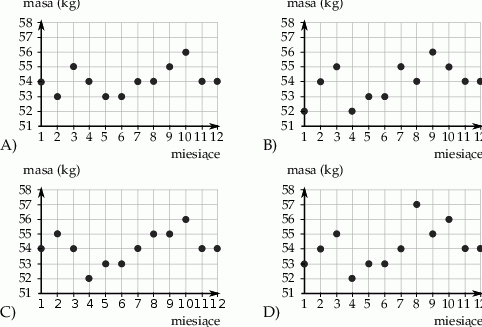
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 129 500 000 zapisana w notacji wykładniczej to
A) 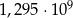 B)
B) 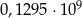 C)
C) 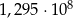 D)
D) 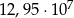
Dane są trzy równania
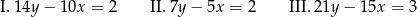
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Układ równań złożony z równań I i III ma jedno rozwiązanie. | P | F |
| Układ równań złożony z równań II i III nie ma rozwiązań. | P | F |
Na wycieczkę szkolną początkowo miało pojechać  chłopców i
chłopców i 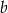 dziewczynek z klasy 5A oraz
dziewczynek z klasy 5A oraz  chłopców i
chłopców i 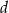 dziewczynek z klasy 6A. Ostatecznie jednak z wycieczki zrezygnowało 10% chłopców z klasy 5A oraz 6 dziewczynek z klasy 6A. Dodatkowo do wycieczki dołączyło 4 chłopców z klasy 6A i 1 dziewczynka z klasy 5A.
dziewczynek z klasy 6A. Ostatecznie jednak z wycieczki zrezygnowało 10% chłopców z klasy 5A oraz 6 dziewczynek z klasy 6A. Dodatkowo do wycieczki dołączyło 4 chłopców z klasy 6A i 1 dziewczynka z klasy 5A.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba uczniów klas 5A i 6A, którzy pojechali na wycieczkę jest równa
A) 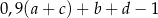 B)
B) 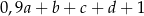
C) 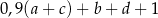 D)
D) 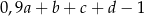
Na rysunku przedstawiono dwie figury. Figura I powstała przez usunięcie trzech kwadratów jednostkowych z kwadratu o boku długości 5, a figura II powstała przez usunięcie czterech kwadratów jednostkowych z prostokąta o bokach długości 3 i 7.
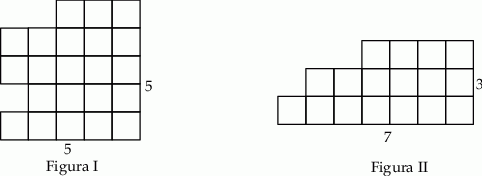
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Obwód figury I jest równy obwodowi figury II. | P | F |
| Obwód figury II jest równy obwodowi kwadratu o boku 5. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Iloraz 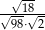 jest równy
jest równy
A) 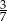 B)
B) 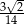 C)
C) 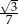 D)
D) 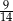
Na osi liczbowej zaznaczono dwa punkty opisane wyrażeniami algebraicznymi.
![]()
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wyrażenie opisujące odległość tych punktów na osi liczbowej jest równe
A) 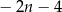 B)
B) 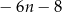 C)
C) 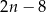 D)
D) 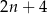
W układzie współrzędnych zaznaczono dwa wierzchołki prostokąta 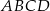 , które nie należą do tego samego boku. Boki tego prostokąta są równoległe do osi układu współrzędnych.
, które nie należą do tego samego boku. Boki tego prostokąta są równoległe do osi układu współrzędnych.
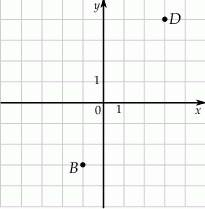
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole prostokąta 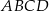 jest równe 28. jest równe 28. | P | F |
Obwód prostokąta 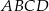 jest równy 11. jest równy 11. | P | F |
W wycieczce szkolnej wzięło udział 12 dziewcząt i 8 chłopców z klasy Va, 13 chłopców i 11 dziewcząt z klasy Vb oraz czworo nauczycieli.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Prawdopodobieństwo, że losowo wybrany uczestnik wycieczki jest chłopcem z klasy Va, jest równe
A)  B)
B) 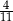 C)
C) 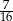 D)
D) 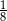
Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.
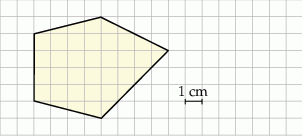
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego wielokąta jest równe
A) 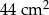 B)
B) 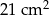 C)
C) 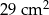 D)
D) 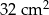
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Graniastosłup może mieć 2019 ścian. | P | F |
| Ostrosłup może mieć 2019 krawędzi. | P | F |
W sześciokąt foremny 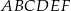 wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
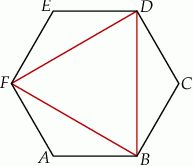
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trójkąta 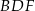 jest większy niż 80% obwodu sześciokąta jest większy niż 80% obwodu sześciokąta 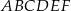 . . | P | F |
Pole trójkąta 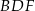 jest 3 razy większe od pola trójkąta jest 3 razy większe od pola trójkąta 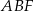 . . | P | F |
Dany jest trójkąt równoramienny 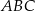 o podstawie długości 10 cm i polu
o podstawie długości 10 cm i polu 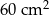 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Ramię trójkąta 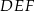 podobnego do trójkąta
podobnego do trójkąta 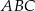 w skali 4:1 ma długość
w skali 4:1 ma długość
A) 52 cm B) 26 cm C) 13 cm D) 48 cm
Na rysunku przedstawiono okrąg o środku 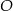 oraz kąt środkowy o mierze
oraz kąt środkowy o mierze 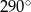 . Punkty
. Punkty 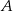 i
i 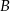 znajdują się na okręgu. Prosta
znajdują się na okręgu. Prosta 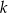 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 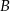 .
.
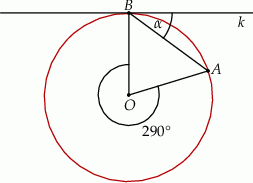
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Miara kąta  jest równa
jest równa
A) 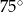 B)
B) 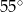 C)
C) 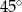 D)
D) 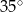
Pole powierzchni całkowitej walca jest równe 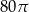 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy.
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wysokość tego walca jest równa
A) 3 B) 6 C) 9 D) 18
W trójkącie 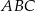 dwusieczna kąta przy wierzchołku
dwusieczna kąta przy wierzchołku 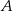 przecina symetralną boku
przecina symetralną boku 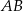 pod kątem
pod kątem 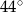 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 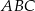 jest trójkątem rozwartokątnym.
jest trójkątem rozwartokątnym.
Właściciel sklepu komputerowego kupił w hurtowni klawiatury i myszki. Cena hurtowa klawiatury była o 30 zł wyższa niż cena hurtowa myszki. Właściciel sklepu ustalił cenę sprzedaży klawiatury o 10% wyższą od ceny hurtowej, a cenę sprzedaży myszki – o 30% wyższą od ceny hurtowej. Klawiatura i myszka łącznie kosztowały w sklepie 213 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej klawiatury i jednej myszki. Zapisz obliczenia.
Z takiego samego rodzaju stearyny wykonano dwie świece: pierwszą w kształcie graniastosłupa prostego o podstawie kwadratu i drugą w kształcie graniastosłupa prostego o podstawie trójkąta równobocznego. Pole podstawy pierwszej świecy jest o 25% większe niż pole podstawy drugiej świecy, a wysokość drugiej świecy jest o 30% większa niż wysokość pierwszej świecy. Łączna waga obu świec to 0,51 kg. Oblicz jaka jest waga każdej ze świec.

