/Szkoła średnia/Zadania maturalne/Matura 2020
Lubelska próba przed maturą
z matematyki poziom podstawowy grupa I 10 marca 2020 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 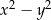 dla
dla 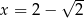 i
i 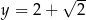 jest równa
jest równa
A) 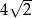 B)
B) 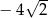 C)
C) 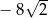 D)
D) 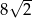
Dana jest liczba 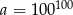 . Liczba
. Liczba 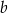 stanowi 1% liczby
stanowi 1% liczby  . Wówczas
. Wówczas
A) 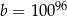 B)
B) 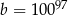 C)
C) 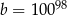 D)
D) 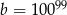
Jeżeli 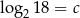 , to liczba
, to liczba 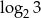 jest równa
jest równa
A) 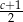 B)
B) 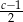 C)
C)  D)
D) 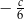
Suma kwadratów dwóch wyrażeń 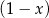 i
i 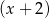 jest równa
jest równa
A) 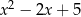 B)
B) 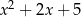 C)
C) 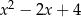 D)
D) 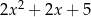
Dziedziną funkcji 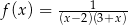 jest zbiór
jest zbiór
A) 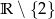 B)
B) 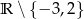 C)
C) 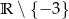 D)
D) 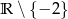
Liczba 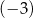 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 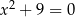 B)
B) 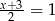 C)
C) 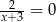 D)
D) 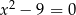
Zbiorem rozwiązań nierówności 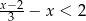 jest przedział
jest przedział
A) 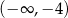 B)
B) 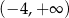 C)
C) 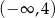 D)
D) 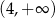
Do wykresu funkcji 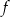 danej wzorem
danej wzorem 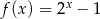 nie należy punkt o współrzędnych
nie należy punkt o współrzędnych
A) 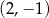 B)
B) 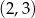 C)
C) 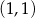 D)
D) 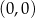
Funkcja kwadratowa 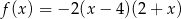 jest malejąca w przedziale
jest malejąca w przedziale
A) 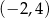 B)
B) 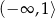 C)
C) 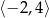 D)
D) 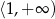
Wykresem funkcji 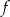 danej wzorem
danej wzorem 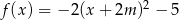 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 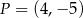 . Wówczas
. Wówczas
A) 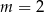 B)
B) 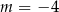 C)
C) 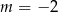 D)
D) 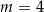
Setny wyraz ciągu 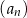 jest równy 2020. Wzór ogólny na
jest równy 2020. Wzór ogólny na  –ty wyraz ciągu
–ty wyraz ciągu 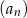 może mieć postać
może mieć postać
A) 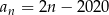 B)
B) 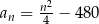 C)
C) 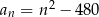 D)
D) 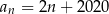
W ciągu arytmetycznym 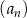 , określonym dla
, określonym dla 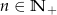 spełniony jest warunek
spełniony jest warunek
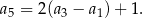
Pierwszy wyraz tego ciągu jest równy
A)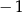 B) 1 C) 2 D) 3
B) 1 C) 2 D) 3
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 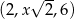 . Wówczas
. Wówczas
A) 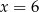 B)
B) 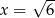 C)
C) 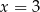 D)
D) 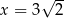
Wiadomo, że 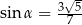 i
i 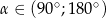 . Wynika stąd, że
. Wynika stąd, że
A) 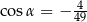 B)
B) 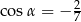 C)
C) 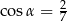 D)
D) 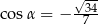
Na okręgu o środku w punkcie 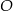 leżą punkty
leżą punkty 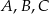 (zobacz rysunek).
(zobacz rysunek).
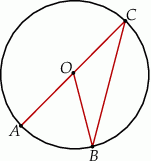
Odcinek 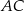 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 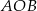 ma miarę
ma miarę 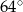 . Kąt
. Kąt 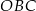 ma miarę równą
ma miarę równą
A) 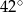 B)
B) 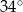 C)
C) 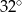 D)
D) 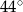
Dwusieczne kątów ostrych trójkąta prostokątnego 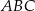 przecinają się w punkcie
przecinają się w punkcie 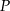 . Przyprostokątne
. Przyprostokątne 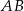 i
i 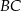 mają długości równe odpowiednio 12 i 9 (zobacz rysunek).
mają długości równe odpowiednio 12 i 9 (zobacz rysunek).
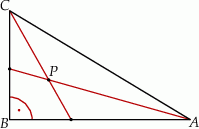
Odległość punktu 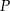 od przeciwprostokątnej
od przeciwprostokątnej 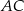 jest równa
jest równa
A) 3 B) 2 C) 15 D) 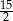
Obwód trójkąta równobocznego jest równy 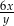 , gdzie
, gdzie 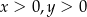 . Pole powierzchni tego trójkąta jest równe
. Pole powierzchni tego trójkąta jest równe
A) 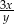 B)
B) 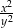 C)
C) 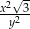 D)
D) 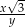
Prosta k o równaniu 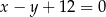 , tworzy z osią
, tworzy z osią 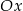 kąt o mierze równej
kąt o mierze równej
A) 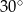 B)
B) 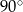 C)
C) 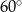 D)
D) 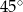
Dłuższy z boków prostokąta 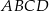 ma długość równą 12, a dwa sąsiednie wierzchołki mają współrzędne
ma długość równą 12, a dwa sąsiednie wierzchołki mają współrzędne 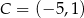 ,
, 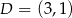 . Pole powierzchni tego prostokąta jest równe
. Pole powierzchni tego prostokąta jest równe
A) 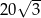 B) 64 C) 80 D) 96
B) 64 C) 80 D) 96
Przekątna graniastosłupa prawidłowego czworokątnego ma długość równą 16 i jest nachylona do płaszczyzny podstawy pod kątem 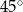 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 8 B) 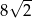 C)
C) 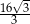 D)
D) 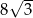
Wysokość ściany bocznej opuszczona na krawędź podstawy ostrosłupa prawidłowego trójkątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej do pola powierzchni podstawy tego ostrosłupa jest równy
A) 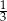 B)
B) 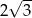 C)
C) 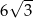 D) 9
D) 9
Ze zbioru cyfr 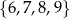 losujemy kolejno bez zwracania dwie cyfry i tworzymy liczbę dwucyfrową. Prawdopodobieństwo tego, że utworzona liczba będzie nie mniejsza niż 89 jest równe
losujemy kolejno bez zwracania dwie cyfry i tworzymy liczbę dwucyfrową. Prawdopodobieństwo tego, że utworzona liczba będzie nie mniejsza niż 89 jest równe
A) 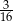 B)
B) 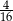 C)
C) 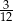 D)
D) 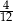
Średnia arytmetyczna zestawu danych: 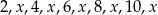 jest równa 4,5. Mediana tego zestawu danych wynosi
jest równa 4,5. Mediana tego zestawu danych wynosi
A) 2 B) 2,5 C) 3 D) 3,5
Pole powierzchni całkowitej sześcianu jest równe 72. Wynika stąd, że przekątna tego sześcianu ma długość równą
A) 6 B) 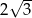 C)
C) 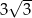 D) 12
D) 12
Aby odblokować telefon komórkowy należy użyć czterocyfrowego kodu PIN. Paweł ustalił, że jego kod PIN na parzystych miejscach będzie miał cyfrę nieparzystą, a na nieparzystych miejscach cyfrę parzystą oraz cyfry nie będą się powtarzać. Ile różnych kodów PIN może utworzyć Paweł?
A) 400 B) 300 C) 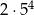 D)
D) 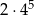
Zadania otwarte
Rozwiąż nierówność 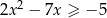 .
.
Uzasadnij, że jeśli 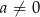 oraz
oraz 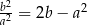 , to
, to 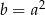 .
.
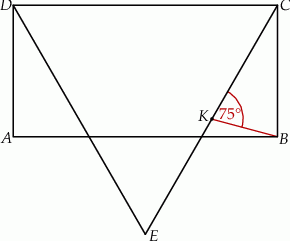
Dany jest prostokąt 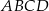 , którego jeden bok jest dwa razy dłuższy od drugiego. Na boku
, którego jeden bok jest dwa razy dłuższy od drugiego. Na boku 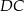 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 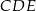 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 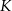 jest takim punktem odcinka
jest takim punktem odcinka 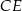 , że
, że 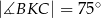 . Udowodnij, że punkt
. Udowodnij, że punkt 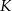 jest środkiem odcinka
jest środkiem odcinka 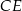 .
.
Ile jest liczb naturalnych dwucyfrowych podzielnych przez 15 lub 20?
Pierwszy wyraz ciągu arytmetycznego jest równy 3, czwarty wyraz tego ciągu jest równy 15. Oblicz sumę sześciu początkowych wyrazów tego ciągu.
Punkty 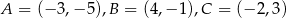 są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
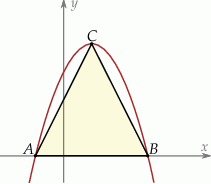
Wierzchołki trójkąta 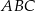 leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej
leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej 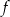 (zobacz rysunek). Pole tego trójkąta jest równe 8, punkt
(zobacz rysunek). Pole tego trójkąta jest równe 8, punkt 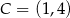 jest wierzchołkiem paraboli, a punkty
jest wierzchołkiem paraboli, a punkty 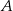 i
i 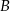 leżą na osi
leżą na osi 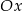 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 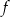 .
.
Dane są dwa pojemniki. W pierwszym z nich znajduje się 9 kul: 4 białe, 3 czarne i 2 zielone. W drugim pojemniku jest 6 kul: 2 białe, 3 czarne i 1 zielona. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo wylosowania dwóch kul tego samego koloru.
Podstawą ostrosłupa 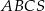 jest trójkąt równoboczny
jest trójkąt równoboczny 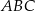 o boku długości 8. Punkt
o boku długości 8. Punkt 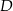 jest środkiem krawędzi
jest środkiem krawędzi 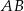 , odcinek
, odcinek 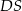 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 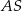 i
i 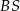 mają długość 7. Oblicz długość krawędzi
mają długość 7. Oblicz długość krawędzi 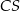 tego ostrosłupa.
tego ostrosłupa.

